www.hydro-pnevmo.ru

Гидравлическое сопротивление. Расчет в Excel.

Опубликовано 24 Июн 2018
Рубрика: Теплотехника | 15 комментариев

Выполнение расчета гидравлического сопротивления отдельного трубопровода и всей системы в комплексе является ключевой задачей в гидравлике,  решение которой позволяет подобрать сечения труб и насос с необходимыми значениями давления и расхода в рабочем режиме.

В одной из ранних статей на блоге рассмотрен простой пример расчета трубопровода с параллельными участками с использованием понятия «характеристика сопротивления». В конце статьи я анонсировал: «Можно существенно  повысить точность метода…». Под этой фразой подразумевалось учесть зависимость характеристик сопротивления от расхода более точно. В том расчете характеристики сопротивлений выбирались из таблиц по диаметру трубы и по предполагаемому расходу. Полковов Вячеслав Леонидович написал взамен таблиц пользовательские функции в Excel для более точного вычисления гидравлических сопротивлений, которые любезно предоставил для печати. Термины «характеристика сопротивления» и «гидравлическое сопротивление» обозначают одно и то же.

Краткая теория.

В упомянутой выше статье теория вкратце рассматривалась. Освежим в памяти основные моменты.

Движение жидкостей по трубам и каналам сопровождается потерей давления, которая складывается из потерь на трение по длине трубопровода и потерь в местных сопротивлениях – в изгибах, отводах, сужениях, тройниках, запорной арматуре и других элементах.

В гидравлике в общем случае потери давления вычисляются по формуле Вейсбаха:

∆Р=ζ·ρ·w²/2, Па, где:

• ζ – безразмерный коэффициент местного сопротивления;
• ρ – объёмная плотность жидкости, кг/м³;
• w – скорость потока жидкости, м/с.

Если с плотностью и скоростью всё более или менее понятно, то определение коэффициентов местных сопротивлений – достаточно непростая задача!

Как было отмечено выше, в гидравлических расчетах принято разделять два вида потерь давления в сетях трубопроводов.

1. В первом случае «местным сопротивлением» считается трение по длине прямого участка трубопровода. Перепад давления для потока в круглой трубе рассчитывается по формуле Дарси-Вейсбаха:

∆Р_тр=ζ_тр·ρ·w²/2=λ·L·ρ·w²/(2·D), Па, где:

• L – длина трубы, м;
• D – внутренний диаметр трубы, м;
• λ – безразмерный коэффициент гидравлического трения (коэффициент Дарси).

Таким образом, при учете сопротивления трению коэффициент потерь – коэффициент местного сопротивления – и коэффициент гидравлического трения связаны для круглых труб зависимостью:

ζ_тр=λ·L/D

2. Во втором случае потери давления в местных сопротивлениях вычисляются по классической формуле Вейсбаха:

∆Р_м=ζ_м·ρ·w²/2, Па

Коэффициенты местных сопротивлений определяются для каждого вида «препятствия» по индивидуальным эмпирическим формулам, полученным из практических опытов.

Выполним ряд математических преобразований. Для начала выразим скорость потока через массовый расход жидкости:

w=G/(ρ·π·D²/4), м/с, где:

• G – расход жидкости, кг/с;
• π – число Пи.

Тогда:

∆Р_тр=8·λ·L·G²/(ρ·π²·D⁵), Па;

∆Р_м=8·ζ_м·G²/(ρ·π²·D⁴), Па.

Введем понятие гидравлических сопротивлений:

S_тр=8·λ·L·/(ρ·π²·D⁵), Па/(кг/с)²;

S_м=8·ζ_м·/(ρ·π²·D⁴), Па/(кг/с)².

∆Р_тр=S_тр·G², Па;

∆Р_м=S_м·G², Па.

Размерность гидравлического сопротивления (Па/(кг/с)²) определена массовой скоростью (кг/с) движения жидкости, а физические процессы в транспортных системах зависят от её объёмной скорости (м³/с), что учтено в формулах присутствием объёмной плотности ρ транспортируемой жидкости.

Для удобства последующих расчётов целесообразно введение понятия «гидравлическая проводимость» — а.

Для последовательного и параллельного соединений гидравлических сопротивлений справедливы формулы:

S_посл=S₁+S₂+…+S_n, Па/(кг/с)²;

S

a_i=(1/S_i)^0,5, (кг/с)/Па^0,5.

Коэффициент гидравлического трения.

Для определения гидравлического сопротивления от трения о стенки трубы S_тр необходимо знать параметр Дарси λ – коэффициент гидравлического трения по длине.

В технической литературе приводится значительное количество формул разных авторов, по которым выполняется вычисление коэффициента гидравлического трения в различных диапазонах значений числа Рейнольдса.

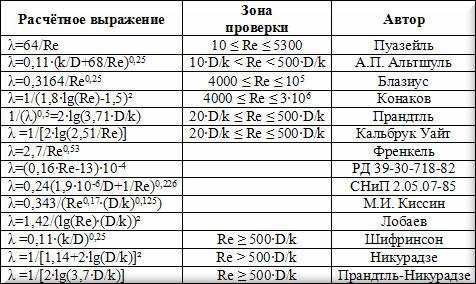
Обозначения в таблице:

• Re – число Рейнольдса;
• k – эквивалентная шероховатость внутренней стенки трубы (средняя высота выступов), м.

В [1] приведена еще одна интересная формула расчета коэффициента гидравлического трения:

λ=0,11·[(68/Re+k/D+(1904/Re)¹⁴)/(115·(1904/Re)¹⁰+1)]^0,25

Вячеслав Леонидович выполнил проверочные расчеты и выявил, что вышеприведенная формула является наиболее универсальной в широком диапазоне чисел Рейнольдса!

Значения, полученные по этой формуле чрезвычайно близки значениям:

• функции λ=64/Re для зоны ламинарного характера потока в диапазоне 10<Re<1500;
• функции λ=0,11·(68/Re+k/D)^0,25для зоны турбулентного характера потока при Re>4500;
• в диапазоне 1500<
  Re<4500 согласно анализу присутствует переходная зона.

В переходной зоне, согласно опытам Никурадзе, график функции λ=f(Re,D,k) имеет сложную форму. Он представляет собой две сопряженные обратные кривые, которые в свою очередь сопрягаются с одной стороны с кривой гладких труб (ламинарный поток), а с другой стороны с прямыми относительной шероховатости.

Данная зона до конца не изучена, поэтому желательно гидравлические режимы проектируемых систем рассчитывать без захода в эту область: 1500<Re<4500!

На следующем рисунке показаны графики функции λ=f(Re,D,k), построенные по вышеприведенной универсальной формуле. Характер кривых в переходной области соответствует графикам Никурадзе [2, 4].

Пользовательская функция в Excel КтрТрубаВода(Р_вода,t_вода,G,D,kэ) выполняет расчет коэффициента гидравлического трения λ по рассмотренной универсальной формуле. При этом везде далее kэ=k.

Внимание!

1. В зоне переходного характера потока происходит смена знака наклона кривой λ, что может вызвать неработоспособность систем автоматического регулирования!
2. ПФ КтрТрубаВода(P_вода,t_вода,G,D,kэ) при турбулентном потоке существенно зависит от значения kэ – эквивалентной шероховатости внутренней поверхности трубы. В связи с этим следует обращать внимание на задание объективного значения kэ с учётом используемых при монтаже труб (см. [2] стр.78÷83).

Расчет в Excel гидравлических сопротивлений.

Для облегчения выполнения рутинных гидравлических расчетов Полковов В.Л. разработал ряд пользовательских функций. Перечень некоторых из них, наиболее часто используемых на практике, приведен в таблице ниже.

Некоторые пояснения по аргументам пользовательских функций:

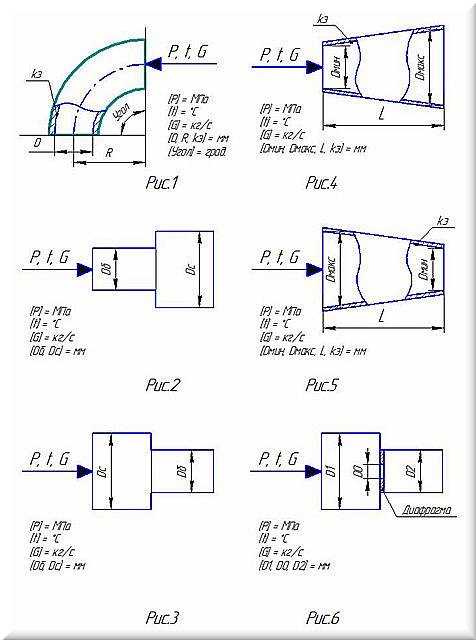
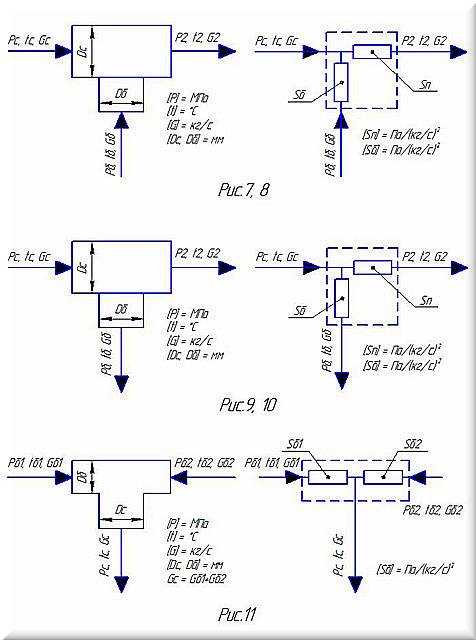
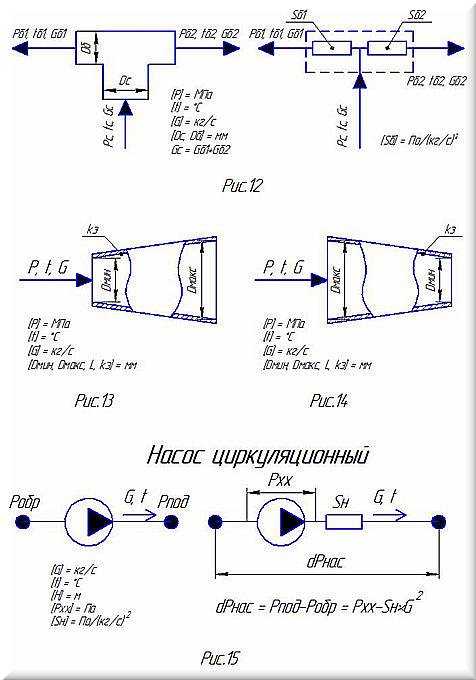
• ГСдиффузор(P_вода,t_вода,G,D_min,D_max,kэ,L) – свободные размеры;
• ГСпереходДиффузор(P_вода,t_вода,G,D_min,D_max,kэ) – стандартный переход;
• ГСконфузор(P_вода,t_вода,G,D_min,D_max,kэ,L) – свободные размеры;
• ГСпереходКонфузор(P_вода,t_вода,G,D_min,D_max,kэ) – стандартный переход;
• ГСотвод(P_вода,t_вода,G,D0,R0,Угол,kэ) – свободные размеры;
• ГСотводГОСТ(P_вода,t_вода,G,D,Угол,kэ) – стандартный отвод.

Приведённые пользовательские функции желательно использовать с учётом начального участка транспортирования (расстояния от одного гидравлического сопротивления до следующего гидравлического сопротивления). Это позволяет уменьшить погрешности расчётов, вызванных влиянием «неустановившегося» характера потока жидкости.

Для турбулентных течений длина начального участка должна быть не менее:

L_нач=(7,88·lg (Re) – 4,35)·D

Для ламинарных течений минимальная длина начального участка:

L_нач=B·Re·D

Здесь В=0,029 по данным Буссинекса, и В=0,065 по данным Шиллера, D — внутренний диаметр системы транспортирования.

Далее на скриншоте показана таблица в Excel с примерами расчетов гидравлических сопротивлений.

Литература:

1. Черникин А.В. Обобщение расчета коэффициента гидравлического сопротивления трубопроводов // Наука и технология углеводородов. М.: 1998. №1. С. 21–23.
2. И.Е. Идельчик, «Справочник по гидравлическим сопротивлениям». 3-е издание, переработанное и дополненное. Москва, «Машиностроение», 1992.
3. А.Д. Альтшуль, «Гидравлические сопротивления», издание второе, переработанное и дополненное. Москва, «НЕДРА», 1982.
4. Б.Н. Лобаев, д.т.н., профессор, «Расчёт трубопроводов систем водяного и парового отопления». Государственное издательство литературы по строительству и архитектуре. УССР, Киев, 1956.

Ссылка на скачивание файла: gidravlicheskie-soprotivleniya (xls 502,0KB).

Другие статьи автора блога

На главную

Статьи с близкой тематикой

Отзывы

al-vo.ru

Расчёт падения давления в трубопроводе

www.ivtechno.ru

Гидравлический расчет простых трубопроводов

6.5. Гидравлический удар

Гидравлическим ударом называется резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении потока рабочей жидкости. Этот процесс является очень быстротечным и характеризуется чередованием резких повышений и понижений давления, которое связано с упругими деформациями жидкости и стенок трубопровода. Гидравлический удар чаще всего возникает при резком открытии или закрытии крана или другого устройства, управляемого потоком.

Пусть в конце трубы, по которой движется жидкость со скоростью υ₀, произведено мгновенное закрытие крана (рис. 6.10, а).

Рис. 6.10. Стадии гидравлического удара

При этом скорость частиц, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдет в работу деформации стенок трубы и жидкости. При этом стенки трубы растягиваются, а жидкость сжимается в соответствии с увеличением давления на величину ΔP_уд, которое называется ударным. Область (сечение n — n), в которой происходит увеличение давления, называется ударной волной. Ударная волна распространяется вправо со скоростью c, называемой скоростью ударной волны.

Когда ударная волна переместится до резервуара, жидкость окажется остановленной и сжатой во всей трубе, а стенки трубы — растянутыми. Ударное повышение давления распространится на всю длину трубы (рис. 6.10, б).

Далее под действием перепада давления ΔP_уд частицы жидкости устремятся из трубы в резервуар, причем это течение начнется с сечения, непосредственно прилегающего к резервуару. Теперь сечение n-n перемещается обратно к крану с той же скоростью c, оставляя за собой выровненное давление P₀ (рис. 6.10, в).

Жидкость и стенки трубы предполагаются упругими, поэтому они возвращаются к прежнему состоянию, соответствующему давлению P₀. Работа деформации полностью переходит в кинетическую энергию, и жидкость в трубе приобретает первоначальную скорость υ₀, но направленную теперь в противоположную теперь сторону.

С этой скоростью весь объем жидкости стремится оторваться от крана, в результате возникает отрицательная ударная волна под давлением P₀ — ΔP_уд, которая направляется от крана к резервуару со скоростью c, оставляя за собой сжавшиеся стенки трубы и расширившуюся жидкость, что обусловлено снижением давления (рис. 6.10, д). Кинетическая энергия жидкости вновь переходит в работу деформаций, но противоположного знака.

Состояние трубы в момент прихода отрицательной ударной волны к резервуару показано на рис. 6.10, е. Так же как и для случая, изображенного на рис. 6.10, б, оно не является равновесным. На рис. 6.10, ж, показан процесс выравнивания давления в трубе и резервуаре, сопровождающийся возникновением движения жидкости со скоростью υ₀.

Очевидно, что как только отраженная от резервуара ударная волна под давлением ΔP _уд достигнет крана, возникнет ситуация, уже имевшая место в момент закрытия крана. Весь цикл гидравлического удара повторится.

Протекание гидравлического удара во времени иллюстрируется диаграммой, представленной на рис. 6.11, а и б.

Штриховыми линиями показано теоретическое изменение давления у крана в точке А, а сплошной действительный вид картины изменения давления по времени (рис. 6.11, а). При этом затухание колебаний давления происходит за счет потерь энергии жидкости на преодоление сил трения и ухода энергии в резервуар.

Если давление P₀ невелико (P₀ P _уд), то картина изменения амплитуды давления получается несколько иная, примерно такая, как показано на рис. 6.11, б.

Рис. 6.11. Изменение давления по времени у крана

Повышение давления при гидравлическом ударе можно определить по формуле

ΔP_уд = ρυ₀c

Данное выражение носит название формулы Жуковского. В нем скорость распространения ударной волны c определится по формуле:

где r — радиус трубопровода;
E — модуль упругости материала трубы;
δ — толщина стенки трубопровода;
K — объемный модуль упругости (см. п.1.3)

Если предположить, что труба имеет абсолютно жесткие стенки, т.е. E = , то скорость ударной волны определится из выражения

Для воды эта скорость равна 1435 м/с, для бензина 1116 м/с, для масла 1200 — 1400 м/с.

6.6. Изменение пропускной способности трубопроводов в процессе их эксплуатации

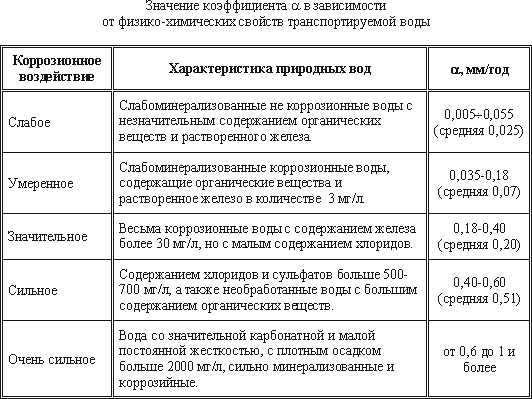
При проектировании напорных трубопроводов следует учитывать, что их пропускная способность в период эксплуатации снижается (например, для водопроводных труб до 50% и даже ниже). Вследствие коррозии и образования отложений в трубах (инкрустации), шероховатость труб увеличивается. Это можно оценить по формуле:

k_t = k₀ + αt

где k₀ — абсолютная шероховатость для новых труб, (мм),
k_t — шероховатость через t лет эксплуатации,
α — коэффициент характеризующий быстроту возрастания шероховатости (мм/год).

Таблица 6.1

Проверить себя ( Тест )

Наверх страницы

gidravl.narod.ru