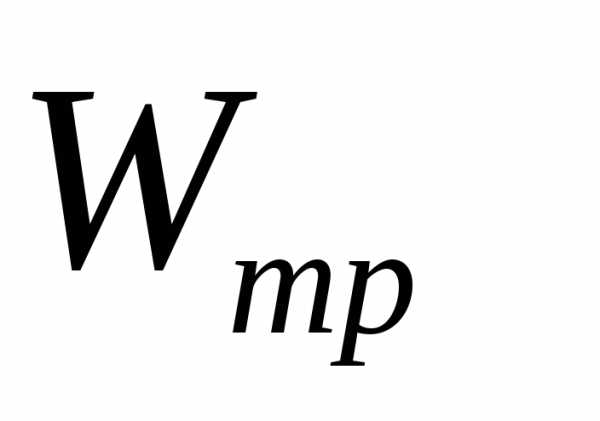Расчет перекрестных балок – . ; ;
Расчет перекрестных балок — Энциклопедия по машиностроению XXL
ПРИБЛИЖЕННЫЙ СПОСОБ РАСЧЕТА ПЕРЕКРЕСТНЫХ БАЛОК [c.381]Заметим, что при взятом нами числе знаков в выражениях для прогибов перекрестных балок третий знак в числах, полученных для моментов, является сомнительным. Конечно, можно было бы получить и более точные выражения для моментов, но такой расчет не имел бы практического значения, так как все решение задачи является по существу лишь приближенным. Мы, например, совершенно не принимали во внимание закона распределения давлений, получаемых балками главного направления от пластины плоского перекрытия, и приняли эти давления равномерно распределенными по плоскости покрытия. На самом деле этого нет, и получаемые вследствие этого погрешности будут в рассмотренном численном примере, вероятно, не меньше тех погрешностей, которые являются следствием неточного определения прогибов перекрестных балок. Выясненный на численном примере способ расчета перекрестных балок легко может быть распространен на тот случай, когда нагрузка неравномерная, а, например, меняется вдоль оси у по линейному закону. Если по концам перекрестных балок приложены моменты, то можно пользоваться тем же приемом расчета нужно только к работе нагрузки присоединить работу опорных пар.
Приближенный способ расчета перекрестных балок. Без указания места публикации, 1916, 8 стр. [c.690]
При исследовании малых прогибов упругих стержней показано, как можно ввести поперечный сдвиг в дифференциальное уравнение равновесия этой теории. Излагается расчет балок на упругом основании и важная для судостроения задача, поставленная И. Г. Бубновым, о расчете перекрестных балок. Рассмотрен продольно-поперечный изгиб балок, приводится точное, а также приближенное, развитое автором, решение в тригонометрических рядах. Дается систематизированное изложение теории выпучивания прямых сплошных стержней, полос, круговых колец, двутавровых балок, устойчивости вала при кручении. Уточняется известная задача Ф. С. Ясинского о расчете на устойчивость пояса открытых мостов. Приводятся точные и приближенные решения этой задачи энергетическим методом, данные самим автором. Особенно ценны результаты, относящиеся к устойчивости плоской формы изгиба полос и двутавровых балок. Теория изгиба, кручения и устойчивости двутавровых балок была разработана автором в 1905—1906 годах и оказалась основополагающим исследованием для последующих разработок в области расчета и общей теории тонкостенных стержней. Автор приводит компактные формулы для расчета критических сил. [c.6]
Расчет перекрестных балок [c.199]
Расчет перекрестных балок 201 [c.201]
Таким образом, мы от изгиба сосредоточенными силами перейдем к изгибу сплошной нагрузкой, распределение которой вдоль перекрестной балки определяется ступенчатой линией (рис. 9). При большом числе балок главного направления мы можем заменить ступенчатую линию плавной кривой и таким образом свести расчет перекрестной балки к исследованию изгиба балки, нагруженной сплошной нагрузкой, изменяющейся по такому закону
Точный расчет поворотной платформы весьма сложен, поэтому обычно ее рассчитывают как систему перекрестных балок, т. е. предполагают, что она состоит из ряда продольных и поперечных балок, шарнирно-уложенных друг на друга (рис. 131, г). Расчет производится по методу сил в предположении равенства перемещений в точке пересечения продольных и поперечных балок в направлении, перпендикулярном плоскости рамы. При ориентировочном определении размеров поворотной платформы ее можно рассматривать как балку, работающую на изгиб под действием вертикальной нагрузки с опасным сечением под передними или задними катками. Для платформы балочной конструкции в расчётное сечение вводят только продольные балки. При этом запасы прочности должны быть максимальными. [c.205]
В. Г. Шухов решил установить минарет на массивный балансир с цилиндрической поверхностью, очерченной радиусом с центром, совмещенным с центром тяжести сооружения. Затем был выполнен точнейший расчет балансира, при котором линейные размеры вычислялись до десятых долей миллиметра, а углы — с точностью до одной секунды. Поворотное устройство выполнялось под наблюдением Владимира Григорьевича. Под его же контролем производились все подготовительные работы перед установкой балансира. Было изготовлено массивное основание из перекрестной системы металлических балок, которое подвели под минарет на уровне фундамента. [c.150]
Все эти усовершенствованные методы расчетов напряженного, состояния в конструкциях судов критически освещены и развиты Петром Федоровичем Папковичем (1887—1946) в труде Строительная механика корабля . В первой его части излагаются вопросы подбора профилей, расчета статически неопределимых балок и плоских рам, составленных из прямых стержней (т. I, стр. 1—618, М., 1945) теория криволинейных рам и перекрестных связей (т. II, стр. 1—816, М.—Л., 1947). Содержание второй части составляют сложный изгиб и устойчивость стержней изгиб и устойчивость пластинок (стр. 1—960, Л., 1941). Эти три тома представляют собой самый полный и современный трактат по строительной механике корабля ).
Результатами последних двух параграфов воспользуемся при расчете перекрестных балок, с которыми приходится встречаться в строительной механике корабля и в некоторых гидротехнических сооружениях. Предположим, что требуется рассчитать плоское перекрытие с прямоугольным контуром, состоящее из пластины и подкрепляющих балок. Нагрузка, воспринимаемая пла-стияой, передается системе равноудаленных балок, которые в дальнейшем будем называть балками главного направления. Эти балки поддерживаются опертой по концам перекрестной балкой АВ (рис. 8). Предположим, что все балки главного направления одинаково нагружены, оперты по концам и имеют одинаковое поперечное сечение. Возьмем одну из этих балок. Пусть Q обозначает ариходящуюся на эту балку сплошную нагрузку, передающуюся от пластины, и Л — реакцию, оказываемую на рассматриваемую балку перекрестной балкой АВ. Прогиб нашей балки в месте соприкасания ее с перекрестной балкой может быть представлен такой формулой [c.199]
Конструкции перекрытий, представляют собой горизонтальные жесткие диски, конструируют по типу балочных клеток с расположением вспомогательных балок с главными в одном уровне. Балки перекрытий работают как разрезные однопролетные или неразрезные мно-гопролегные системы, а в некоторых случаях как системы перекрестных балок или ферм. Методика расчета изгибаемых элементов должна быть с учетом их расчетной схемы. По аналогии производят расчет элементов ростверка и поддерживающих балок или ферм.
Работая над созданием барж с лучшими ходовыми качествами, устанавливая наивыгоднейшие основные размеры и находя рациональные очертания их остова, определяющие хорошую обтекаемость и максимальную грузоподъемность при малой осадке, В.Г. Шухов одновременно добивался конструктивной простоты. Поперечное сечение баржи, построенной в 1894 г. по заказу общества Меркульевы , представляет собой почти правильный прямоугольник. Две идущие вдоль баржи переборки из сплошного металлического листа создают три продольных отсека, которые в свою очередь разделяются рядом поперечных переборок. Переборки используются в качестве несущих диафрагм, и для придания им необходимой жесткости на них наклепаны стойки и перекрестные раскосы. Таким образом, Шухов создавал своеобразную кессонную систему из перекрещивающихся высоких продольных и поперечных балок со сплошными стенками. Внутренний отсек между двумя продольными переборками выполнен как жесткий ростверк, образуемый по дну продольными (кильсонными) и поперечными (шпангоут-ными) балками ). Каждая из металлических переборок, отделяющих друг от друга отсеки баржи, так же как и обшивка ее корпуса, играла не только роль конструктивно необходимого элемента. В.Г. Шухов умело использовал в расчете несущую способность этих элементов. получая, таким образом, значительную экономию в металле. [c.128]
В проектировании судов большое значение имеет теория плоских перекрытий из перекрестных продольных и поперечных балок, и Бубнов много сделал для разработки этой теории. Рассматривая систему параллельных равноотстоящих продольных балок, опирающихся на поперечную балку, Бубнов показал, что эту и тe -му можно трактовать как балку на упругом основании, и для проведения расчета именно по этому способу составил таблицы для [c.525]
Предположим, что требуется рассчитать плоское перекрытие (рис. 1) с прямоугольным контуром, состоящее из тонкой пластины и подкрепляющих балок. Нагрузка, воспринимаемая пластиной, передается системе равноудаленных вертикальных балок, которые в дальнейщем бу- Л В дем называть балками главного направления. Эти балки поддерживаются несколькими горизонтально расположенными перекрестными балками. Расчет такой системы балок представляет задачу статически неопределимую с больщим числом лищних неизвестных.
mash-xxl.info
Расчет несущей способности и прогиба деревянных балок
Чтобы построить деревянный дом необходимо провести расчёт несущей способности деревянной балки. Также особое значение в строительной терминологии имеет определение прогиба.
Без качественного математического анализа всех параметров просто невозможно построить дом из бруса. Именно поэтому перед тем как начать строительство крайне важно правильно рассчитать прогиб деревянных балок. Данные расчёты послужат залогом вашей уверенности в качестве и надёжности постройки.
Что нужно для того чтобы сделать правильный расчёт
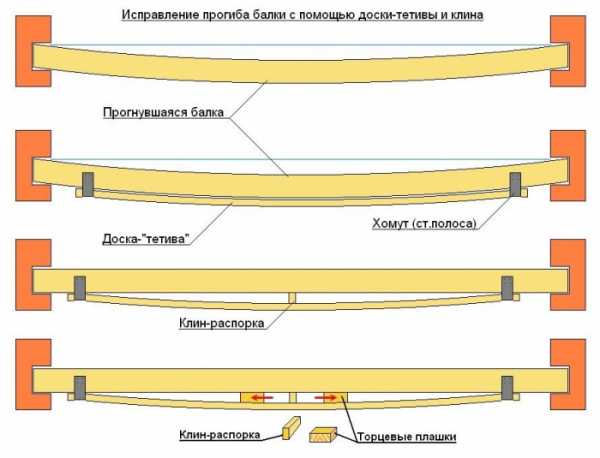
Расчёт несущей способности и прогиба деревянных балок не такая простая задача, как может показаться на первый взгляд. Чтобы определить, сколько досок вам нужно, а также, какой у них должен быть размер необходимо потратить немало времени, или же вы просто можете воспользоваться нашим калькулятором.
Во-первых, нужно замерить пролёт, который вы собираетесь перекрыть деревянными балками. Во-вторых, уделите повышенное внимание методу крепления. Крайне важно, насколько глубоко фиксирующие элементы будут заходить в стену. Только после этого вы сможете сделать расчёт несущей способности вместе с прогибом и ряда других не менее важных параметров.
Длина

Перед тем как рассчитать несущую способность и прогиб, нужно узнать длину каждой деревянной доски. Данный параметр определяется длиной пролёта. Тем не менее это не всё. Вы должны провести расчёт с некоторым запасом.
Важно! Если деревянные балки заделываться в стены — это напрямую влияет на их длину и все дальнейшие расчёты.
При подсчёте особое значение имеет материал, из которого сделан дом. Если это кирпич, доски будут монтироваться внутрь гнёзд. Приблизительная глубина около 100—150 мм.
Когда речь идёт о деревянных постройках параметры согласно СНиПам сильно меняются. Теперь достаточно глубины в 70—90 мм. Естественно, что из-за этого также изменится конечная несущая способность.
Если в процессе монтажа применяются хомуты или кронштейны, то длина брёвен или досок соответствует проёму. Проще говоря, высчитайте расстояние от стены до стены и в итоге сможете узнать несущую способность всей конструкции.
Важно! При формировании ската крыши брёвна выносятся за стены на 30—50 сантиметров. Это нужно учесть при подсчёте способности конструкции противостоять нагрузкам.
К сожалению, далеко не всё зависит от фантазии архитектора, когда дело касается исключительно математики. Для обрезной доски максимальная длина шесть метров. В противном случае несущая способность уменьшается, а прогиб становится больше.
Само собой, что сейчас не редкость дома, у которых пролёт достигает 10—12 метров. В таком случае используется клееный брус. Он может быть двутавровым или же прямоугольным. Также для большей надёжности можно использовать опоры. В их качестве идеально подходят дополнительные стены или колоны.

Совет! Многие строители при необходимости перекрыть длинный пролёт используют фермы.
Общая информация по методологии расчёта
В большинстве случаев в малоэтажном строительстве применяются однопролётные балки. Они могут быть в виде брёвен, досок или брусьев. Длина элементов может варьироваться в большом диапазоне. В большинстве случаев она напрямую зависит от параметров строения, которые вы собираетесь возвести.
Внимание! Представленный в конце странички калькулятор расчета балок на прогиб позволит вам просчитать все значения с минимальными затратами времени. Чтобы воспользоваться программой, достаточно ввести базовые данные.
Роль несущих элементов в конструкции выполняют деревянные бруски, высота сечения которых составляет от 140 до 250 мм, толщина лежит в диапазоне 55—155 мм. Это наиболее часто используемые параметры при расчёте несущей способности деревянных балок.
Очень часто профессиональные строители для того чтобы усилить конструкцию используют перекрёстную схему монтажа балок. Именно эта методика даёт наилучший результат при минимальных затратах времени и материалов.
Если рассматривать длину оптимального пролёта при расчёте несущей способности деревянных балок, то лучше всего ограничить фантазию архитектора в диапазоне от двух с половиной до четырёх метров.
Внимание! Лучшим сечением для деревянных балок считается площадь, у которой высота и ширина соотносятся как 1,5 к 1.
Как рассчитать несущую способность и прогиб

Стоит признать, что за множество лет практики в строительном ремесле был выработан некий канон, который чаще всего используют для того, чтобы провести расчёт несущей способности:
M/W<=Rд
Расшифруем значение каждой переменной в формуле:
- Буква М вначале формулы указывает на изгибающий момент. Он исчисляется в кгс*м.
- W обозначает момент сопротивления. Единицы измерения см3.
Расчёт прогиба деревянной балки является частью, представленной выше формулы. Буква М указывает нам на данный показатель. Чтобы узнать параметр применяется следующая формула:
M=(ql2)/8
В формуле расчёта прогиба есть всего две переменных, но именно они в наибольшей степени определяют, какой в конечном итоге будет несущая способность деревянной балки:
- Символ q показывает нагрузку, которую способна выдержать доска.
- В свою очередь буква l — это длина одной деревянной балки.
Внимание! Результат расчёт несущей способности и прогиба зависит от материала из которого сделана балка, а также от способа его обработки.
Насколько важно правильно рассчитать прогиб

Этот параметр крайне важен для прочности всей конструкции. Дело в том, что одной стойкости бруса недостаточно для долгой и надёжной службы, ведь со временем его прогиб под нагрузкой может увеличиваться.
Прогиб не просто портит эстетичный вид перекрытия. Если данный параметр превысит показатель в 1/250 от общей длины элемента перекрытия, то вероятность возникновения аварийной ситуации возрастёт в десятки раз.
Так зачем нужен калькулятор
Представленный ниже калькулятор позволит вам моментально просчитать прогиб, несущую способность и многие другие параметры без использования формул и подсчётов. Всего несколько секунд и данные по вашему будущему дому будут готовы.
bouw.ru
Балки перекрестные — Энциклопедия по машиностроению XXL
В течение 50—60-х гг. мировая практика накопила огромный опыт в развитии современных металлических конструкций. Были разработаны конструкции массового применения в виде традиционных балок, ферм и колонн для одноэтажных и многоэтажных промышленных и гражданских зданий, а также новые типы эффективных конструкций — предварительно напряженные фермы и балки, перекрестно-стержневые конструкции, вантовые и мембранные конструкции, сетчатые купола, своды и др. [c.7]I 9. Балки расположены перекрестно, как показано на рисунках. [c.132]
Стальная балка швеллерного сечения № 8 длиной 3 м, сжатая силами Р, скреплена с двумя перекрестными балками тех же размеров. Сколько полуволн должно образоваться по потере устойчивости Определить критическую нагрузку пользуясь графиком, данным в решении задачи 8.39. [c.206]
Отсюда критическая нагрузка Р р = 2,3-3640 == 8350 кГ. Критическая жесткость опор соответствует значению с//Рэ = 81, Получае.м необходимый момент инерции перекрестной балки У, из уравнения [c.390]
Типы металлических составных стержней показаны на рис. 1—3. На рис. 1 приведены наиболее употребительные типы металлических составных колонн. Для элементов, работающих на поперечный изгиб, характерны составные клепаные или сварные балки (рис. 2). Составляющими стержнями в них следует считать поясные листы, поясные уголки и стенку балки. К составным стержням можно отнести также растянутые или сжатые пакеты, стыкованные по длине внахлестку. Сюда относятся ступенчатые, универсальные и перекрестные клепаные стыки (рис. 3). [c.5]
Перекрестная связь — связь, образуемая двумя перекрещивающимися балками, работающими на изгиб и подкрепляющими подвергаемый кручению пространственный каркас прямоугольного сечения. [c.14]
Жесткость дополнительных крестообразных связей, показанных на рис. 7.4, можно оценить, если рассматривать крестообразную связь как две балки с заделанными концами, каждая из которых нагружает другую в середине длины пролета. Прогиб в середине-длины каждой перекрестной балки [c.167]
Балки расположены перекрестно, как показано на рисунках, В местах пересечения балок при отсутствии нагрузки низ верхних балок касается верха нижних балок без нажима. Размеры балок обозначены на рисунке, причем [c.240]
В качестве примера рассмотрим изгиб перекрестной балки АВ, [c.192]
Через посредство обшивки на систему балочек передается равномерно распределенная нагрузка. Пусть Q — нагрузка, приходящаяся на одну балочку. Если бы балка А В была абсолютно жесткой и пересекала вертикальные балки посредине пролета, то давление от каждой из балочек, передаваемое перекрестной балке АВ, равнялось бы — -Q. Вследствие прогиба перекрестной балки давление [c.192]
Сосредоточенное давление R заменим сплошной нагрузкой, распределенной равномерно на протяжении d, равном расстоянию между вертикальными балочками. При значительном числе вертикальных балочек такая замена не произведет значительного влияния на прогиб балки Л 5, и мы можем с достаточной точностью считать, что на перекрестную балку АВ передается сплошная нагрузка, распределенная по закону [c.192]
Увеличивая жесткость перекрестной балки, мы тем самым уменьшаем величину /С и, следовательно, увеличиваем давление R в [c.193]
Если р обозначает число балок главного направления, г — число перекрестных балок, EJ[ — жесткость i-й балки главного направления и EJJ—жесткость /-й перекрестной балки, то потенциальная энергия изгиба нашей системы балок представится выражением [c.382]
Имея выражение для коэффициентов, легко найти прогиб любой перекрестной балки. Предположим, например, что у нас число перекрестных балок нечетное, и напишем уравнение изогнутой оси для средней балки, которой соответствует yr+i = lj2. Вставляя это [c.384]
Наибольшую роль играет первый член этого выражения и обыкновенно в качестве первого приближения им можно ограничиться. Тогда можно сказать, что прогиб рассматриваемой перекрестной балки такой же, как у балки с опертыми концами, лежащей на сплош- [c.384]
Мы до сих пор предполагали, что все перекрестные балки имеют одинаковую жесткость, такое же допущение мы делали и относительно балок главного направления, но тот же прием может быть с выгодой применен и в тех случаях, когда одной или нескольким балкам придано иное сечение. Ход решения задачи поясним на таком примере. Предположим, что плоское покрытие, несущее равномерную нагрузку, поддерживается одиннадцатью равноудаленными балками главного направления и пятью перекрестными балками. Концы всех балок предполагаются свободно поворачивающимися. Поперечные сечения всех балок главного направления одинаковы. [c.385]
Имея значения коэффициентов а п, легко написать выражение для изогнутой оси каждой перекрестной балки. [c.387]
Так, например, для средней перекрестной балки (i/=/i/2) получим [c.387]
Величину изгибающего момента для каждой перекрестной балки найдем из формулы i) [c.387]
Заметим, что при взятом нами числе знаков в выражениях для прогибов перекрестных балок третий знак в числах, полученных для моментов, является сомнительным. Конечно, можно было бы получить и более точные выражения для моментов, но такой расчет не имел бы практического значения, так как все решение задачи является по существу лишь приближенным. Мы, например, совершенно не принимали во внимание закона распределения давлений, получаемых балками главного направления от пластины плоского перекрытия, и приняли эти давления равномерно распределенными по плоскости покрытия. На самом деле этого нет, и получаемые вследствие этого погрешности будут в рассмотренном численном примере, вероятно, не меньше тех погрешностей, которые являются следствием неточного определения прогибов перекрестных балок. Выясненный на численном примере способ расчета перекрестных балок легко может быть распространен на тот случай, когда нагрузка неравномерная, а, например, меняется вдоль оси у по линейному закону. Если по концам перекрестных балок приложены моменты, то можно пользоваться тем же приемом расчета нужно только к работе нагрузки присоединить работу опорных пар. [c.388]
Здесь через 1 обозначен пролет и через Е/ — жесткость балок главного направления. Соответствующие величины для перекрестной балки обозначим через I ж Е1. [c.199]
Перекрестная балка изгибается давлениями В, приложенными в местах пересечения ее с балками главного направления. Давления эти на основании (а) могут быть представлены так [c.199]
Они имеют наименьшее значение в местах наибольшего прогиба перекрестной балки, т. е. у середины пролета АВ, 1 достигают наибольшей величины у концов перекрестной балки, где прогибы малы. Вычисление давлений Л, связанное с определением прогибов, мы выполним [c.199]
Таким образом, мы от изгиба сосредоточенными силами перейдем к изгибу сплошной нагрузкой, распределение которой вдоль перекрестной балки определяется ступенчатой линией (рис. 9). При большом числе балок главного направления мы можем заменить ступенчатую линию плавной кривой и таким образом свести расчет перекрестной балки к исследованию изгиба балки, нагруженной сплошной нагрузкой, изменяющейся по такому закону [c.200]
Дифференциальное уравнение изогнутой оси перекрестной балки записывается так [c.200]
Результатами последних двух параграфов воспользуемся при расчете перекрестных балок, с которыми приходится встречаться в строительной механике корабля и в некоторых гидротехнических сооружениях. Предположим, что требуется рассчитать плоское перекрытие с прямоугольным контуром, состоящее из пластины и подкрепляющих балок. Нагрузка, воспринимаемая пла-стияой, передается системе равноудаленных балок, которые в дальнейшем будем называть балками главного направления. Эти балки поддерживаются опертой по концам перекрестной балкой АВ (рис. 8). Предположим, что все балки главного направления одинаково нагружены, оперты по концам и имеют одинаковое поперечное сечение. Возьмем одну из этих балок. Пусть Q обозначает ариходящуюся на эту балку сплошную нагрузку, передающуюся от пластины, и Л — реакцию, оказываемую на рассматриваемую балку перекрестной балкой АВ. Прогиб нашей балки в месте соприкасания ее с перекрестной балкой может быть представлен такой формулой [c.199]
Две перекрестные балки длиной li и нагружены посе- редине силой Р. Найти распределение нагрузки между балками. Моменты инерции сечений балок соответственно Ji и У . Материал. балок одинаковый. [c.137]
Две перекрестные балки одинаковой длины / и равной жесткости EJ шарнирно оперты по концам, соединены ме вду собой лосередине. Одна из балок сжата силой Я, а вторая— силой kP, [c.207]
Балки из композиционных материалов могут быть многослойные и трехслойные. Можно привести множество примеров многослойных балок от простого короткого образца для испытаний до более сложных двутавровых балок переменного сечения (рис. 15) или искривленных балок (рис. 16). Конфигурация трехслойных балок также может изменяться в пшроких (хотя и не до такой степени) пределах — от образца для испытаний (рис. 17) до перекрестных балок и панелей переменной толщины. [c.133]
Сборная предварительно напряженная железобетонная оболочка положительной кривизны с размерами в плане 102×102 м построена в г. Челябинске [1]. Оболочка собрана пз ребристых панелей размером 298X1195 см, укладывающихся на перекрестную систему тавровых железобетонных балок (рис. 2.14). Панели по контуру окаймлены ребрами, высота которых у опорной зоны составляла 34 см, в середине пролета — 43 см. Кроме того, плита панелей толщиной 5 см подкреплена тремя поперечными ребрами. Балки длиной 1180 см, на которые укладывались плиты, имели переменную высоту 75 см у края, 88 см в середине пролета. [c.73]
Работая над созданием барж с лучшими ходовыми качествами, устанавливая наивыгоднейшие основные размеры и находя рациональные очертания их остова, определяющие хорошую обтекаемость и максимальную грузоподъемность при малой осадке, В.Г. Шухов одновременно добивался конструктивной простоты. Поперечное сечение баржи, построенной в 1894 г. по заказу общества Меркульевы , представляет собой почти правильный прямоугольник. Две идущие вдоль баржи переборки из сплошного металлического листа создают три продольных отсека, которые в свою очередь разделяются рядом поперечных переборок. Переборки используются в качестве несущих диафрагм, и для придания им необходимой жесткости на них наклепаны стойки и перекрестные раскосы. Таким образом, Шухов создавал своеобразную кессонную систему из перекрещивающихся высоких продольных и поперечных балок со сплошными стенками. Внутренний отсек между двумя продольными переборками выполнен как жесткий ростверк, образуемый по дну продольными (кильсонными) и поперечными (шпангоут-ными) балками ). Каждая из металлических переборок, отделяющих друг от друга отсеки баржи, так же как и обшивка ее корпуса, играла не только роль конструктивно необходимого элемента. В.Г. Шухов умело использовал в расчете несущую способность этих элементов. получая, таким образом, значительную экономию в металле. [c.128]
Частоты свободных колебаний открытой решетки (перекрытия) с большим числом одинаковых и равноотстоящих балок одного из направлений ( главное направлениел) и с несколькими перекрестными связями, одинаково установленными на опорах (рис. 13), совпадают с частотами изолированной балки главного направления, несущей сосредоточенные массы в точках пересечения с перекрестными балками, и опирающейся в этих точках на упругие опоры с жесткостью Кы (рис> 14). Прнчсм [c.450]
В проектировании судов большое значение имеет теория плоских перекрытий из перекрестных продольных и поперечных балок, и Бубнов много сделал для разработки этой теории. Рассматривая систему параллельных равноотстоящих продольных балок, опирающихся на поперечную балку, Бубнов показал, что эту и тe -му можно трактовать как балку на упругом основании, и для проведения расчета именно по этому способу составил таблицы для [c.525]
Предположим, что требуется рассчитать плоское перекрытие (рис. 1) с прямоугольным контуром, состоящее из тонкой пластины и подкрепляющих балок. Нагрузка, воспринимаемая пластиной, передается системе равноудаленных вертикальных балок, которые в дальнейщем бу- Л В дем называть балками главного направления. Эти балки поддерживаются несколькими горизонтально расположенными перекрестными балками. Расчет такой системы балок представляет задачу статически неопределимую с больщим числом лищних неизвестных. [c.381]
Рассмотрим подробнее случай, когда балки главного направления равноудалены и имеют одинаковое поперечное сечение. Те же предположения сделаем относительно перекрестных балок и допустим, что система балок изгибается равномерно распределенной нагрузкой интенсивности q. Из условий симметрии можем заключить, что в общее выражение (3) для прогиба войдут лишь члены с нечетными значками m и п, и уравнения для определения коэффициентов Ujnn, получаемые из общего выражения (Ь), будут иметь такой вид 1=р [c.383]
Здесь через Q обозначена величина qlil/(p+l), представляющая собой нагрузку, приходящуюся на одну балку главного направления. Множитель, стоящий перед скобками в полученном выражении для прогиба перекрестной балки, с достаточной точностью может быть принят равным прогибу балки главного направления при отсутствии перекрестных балок. Множителем 1—фо(ы) оценивается влияние перекрестных балок. На основании таблицы значений функции фо(ы) заключаем, что при я/2главного направления, но, наоборот, увеличивают ее прогиб. Когда прогибы перекрестных балок определены намеченным здесь способом, легко может быть рассчитана средняя балка главного направления. Для этого проще всего воспользоваться формулами для неразрезной балки с опорами, расположенными на различных высотах. [c.385]
mash-xxl.info
Дача и Дом — Расчет балок перекрытия
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/helper.php on line 274
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/helper.php on line 110
Strict Standards: call_user_func_array() expects parameter 1 to be a valid callback, non-static method modIceMegamenuHelper::buildXML() should not be called statically in /home/content/79/5851379/html/dacha/libraries/joomla/cache/controller/callback.php on line 159
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 72
Strict Standards: Non-static method JSite::getMenu() should not be called statically in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/helper.php on line 47
Strict Standards: Non-static method JApplication::getMenu() should not be called statically in /home/content/79/5851379/html/dacha/includes/application.php on line 536
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/helper.php on line 47
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/helper.php on line 68
Strict Standards: Declaration of JParameter::loadSetupFile() should be compatible with JRegistry::loadSetupFile() in /home/content/79/5851379/html/dacha/libraries/joomla/html/parameter.php on line 512
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/libs/menucore.php on line 277
Deprecated: Non-static method JSite::getMenu() should not be called statically, assuming $this from incompatible context in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/helper.php on line 120
Deprecated: Non-static method JApplication::getMenu() should not be called statically, assuming $this from incompatible context in /home/content/79/5851379/html/dacha/includes/application.php on line 536
Strict Standards: Only variables should be assigned by reference in /home/content/79/5851379/html/dacha/modules/mod_icemegamenu/helper.php on line 120
www.dacha-dom.ru
Прочность корпуса водного транспорта
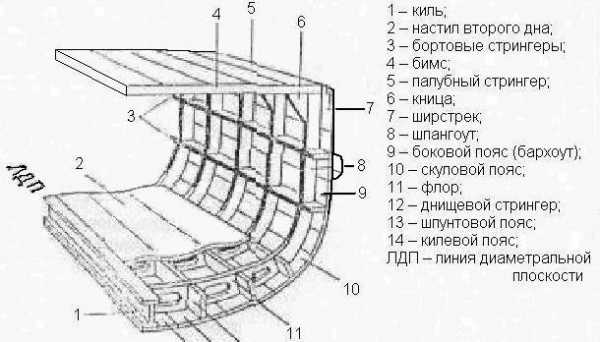 При расчете на местную прочность отдельные конструкции корпуса судна представляются в виде перекрытий, рам, изолированных балок и пластин.
При расчете на местную прочность отдельные конструкции корпуса судна представляются в виде перекрытий, рам, изолированных балок и пластин.
Перекрытие — это система пересекающихся и взаимно связанных балок, концы которых закреплены на так называемом опорном контуре. Опорный контур днищевых и палубных перекрытий образуют борта судна и поперечные переборки, опорный контур бортовых перекрытий — поперечные переборки, днище и палуба судна.
Балки перекрытия располагают параллельно сторонам опорного контура (рис. 1, а). Те балки, которых в перекрытии больше, называются балками главного направления; балки, перпендикулярные им, называются перекрестными балками.
При расчете перекрытия полагают, что нагрузка воспринимается балками главного направления и передается перекрестным балкам, которые должны иметь достаточную жесткость, так как они предназначены для разгрузки балок главного направления. Если жесткость перекрестных балок мала, то они могут даже загружать балки главного направления, что иногда используется для разнесения сосредоточенных нагрузок на большее число балок главного направления.
Днищевые перекрытия рассчитывают на действие нагрузки от гидростатического давления забортной воды, веса грузов, оборудования и механизмов, находящихся на днище. Нагрузка должна соответствовать тому положению судна на волне, для которого вычислены напряжения от общего изгиба.
Расчет бортовых перекрытий производят на гидростатическую нагрузку, распределенную по треугольнику и отвечающую положению судна на волне. Местная прочность связей палубного перекрытия проверяется на действие равномерно распределенной нагрузки от веса находящегося на палубе груза и веса воды, попадающей на палубу во время шторма. Нагрузки, на которые рассчитываются перекрытия, регламентируются «Нормами прочности морских судов».
Если число балок обоих направлений небольшое, то перекрытия рассчитывают методом приравнивания прогибов. При нескольких перекрестных балках расчет перекрытия может быть сведен к расчету балок главного направления, загруженных реакциями со стороны перекрестных связей и внешней нагрузкой (рис.1, а). Если число балок главного направления велико, то они как бы создают для перекрестных балок упругое основание. В этом случае расчет перекрытия сводится к расчету перекрестных балок на упругом основании.
Конструктивные элементы и связи корпуса судна:
а — ахтерпиковая переборка, b — коробчатая балка, с — надстройка, d — носовая оконечность, е — кормовая оконечность, f — район грузового люка, g — район между грузовыми люками, h — район машинного отделения, i — главная палуба в районе угла грузового люка 1 — палуба ахтерпиковой цистерны; 2 — дейдвудная труба; 3 — верхний пояс обшивки; 4 — стенка; 5 — нижний пояс обшивки; 6 — настил палубы; 7 — продольный комингс люка; 8 — поперечный комингс люка; 9 — ширстрек; 11 — скуловой пояс; 12 — настил второго дна; 13 — днищевая обшивка; 14 — цепной ящик; 15 — твиндек; 16 — таранная переборка; 17 — ют; 18 — аварийный выход; 19 — ахтерпик; 20 — гребной вал; 21 — дейдвудная труба; 22 — ахтерштевень; 23 — перо руля; 24 — баллер руля; 25 — бак; 26 — форпик; 27 — бортовой стрингер; 28 — твиндечный шпангоут; 29 — трюмный шпангоут; 30 — верх-ная (главная) палуба; 31 — туннель гребного вала; 32 — карлингсы; 33 — днищевые стрингеры; 34 — вертикальный киль; 35 — машинная шахта; 36 — верхний световой люк; 37 — навигационный мостик; 38 — шлюпочная палуба; 39 — палуба средней надстройки; 40 — верхняя (главная) палуба; 41 — фундамент главного двигателя; 42 — шпангоут надстройки; 43 — крайний междудонный лист; 44 — рамный бимс; 45 — рамный шпангоут; 46 — ромбоидальный лист-накладка; 47 — пиллерс; 48 — носовые брештуки; 49 — продольное ребро.
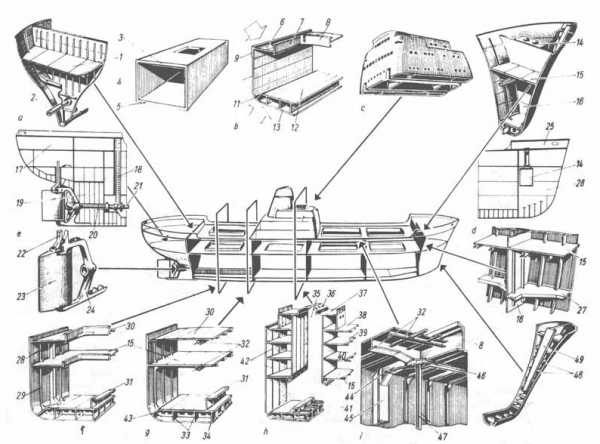
Под рамами понимают балки набора, расположенные в одной плоскости и жестко соединенные между собой. На рис. 1, б показаны схемы шпангоутных рам однопалубного и двухпалубного судна. Рамы состоят из флора, шпангоутов и бимсов. Поскольку у промысловых судов флоры значительно больше шпангоутов, полагают, что шпангоуты жестко заделаны на флорах, и производят расчет шпангоутных рам без днищевых ветвей (рис. 1, б). Шпангоутные рамы однопалубных судов рассчитывают методом трех моментов, многопалубных судов — методом угловых деформаций. Расчетной является гидростатическая нагрузка, распределенная по всей высоте борта по закону треугольника.
Изолированные балки — это такие балки, прочность которых может быть рассчитана отдельно от прочности перекрытия. Они намного меньше других связей перекрытия. К числу изолированных балок относятся, например, ребра жесткости, установленные по днищу между флорами. Вследствие симметрии конструкции и нагрузки такие ребра жесткости рассчитывают как балки, жестко заделанные на флорах и загруженные давлением воды (рис. 1, в).
Под пластинами понимают части листов наружной обшивки, настилов палуб, платформ и двойного дна между балками набора (рис. 1, г). Балки набора служат для пластины опорным контуром. Как правило, пластины имеют симметричные пролеты и нагрузку, поэтому их можно считать жестко заделанными на опорном контуре. Если отношение сторон опорного контура велико, то пластину можно полагать гнущейся в средней части по цилиндрической поверхности. В этом случае расчет пластины сводится к расчету балки единичной ширины, вырезанной из пластины вдоль короткой стороны.
Поскольку пластины участвуют в изгибе вместе с балками набора, в расчетное сечение балок включают части пластин, прилегающие к балкам—так называемые присоединенные пояски. Ширина присоединенного пояска определяется по «Нормам прочности».
В связях, участвующих одновременно в обеспечении общей и местной прочности, производится суммирование напряжений от общего и местного изгибов. Например, в днищевой обшивке суммируются напряжения от общего изгиба, изгиба днищевой пластины вместе с продольными балками набора и изгиба самой пластины. Напряжения от местного изгиба позволяют оценить местную прочность судовых конструкций, а суммарные напряжения от общего и местного изгибов — общую прочность корпуса судна.
seaman-sea.ru
6.4. Расчет балок
Подбор сечения металлических прокатных балок сводится к определению по максимальному изгибающему моменту Mmax номера профиля двутавра или швеллера и к определению прогиба балки f. Указанный расчет достаточен при архитектурном проектировании. (Детальный расчет включает еще проверку общей устойчивости и местных напряжений).
Прокатные балки рассчитывают в такой последовательности:
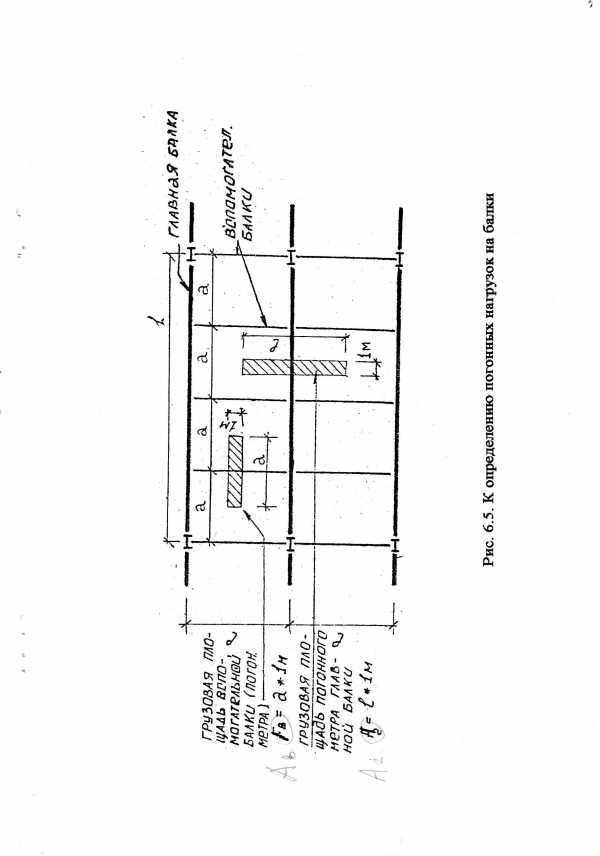
Определяют нагрузки на балки.
Определяют внутренние усилия изгибаюший момент М и поперечную силу Q.
Определяют требуемый момент сопротивления по формуле
И далее по сортаменту определяют номер профиля.
Производят проверку по касательным напряжениям по формуле
Значения
касательных напряжений  в сечениях изгибаемых элементов должны
удовлетворять условию
в сечениях изгибаемых элементов должны
удовлетворять условию

где Q — максимальная поперечная сила, S — статический момент площади полусечения, I—
момент инерции сечения балки,
t–толщина
стенки, Rs-расчетное
сопротивление металла срезу; а 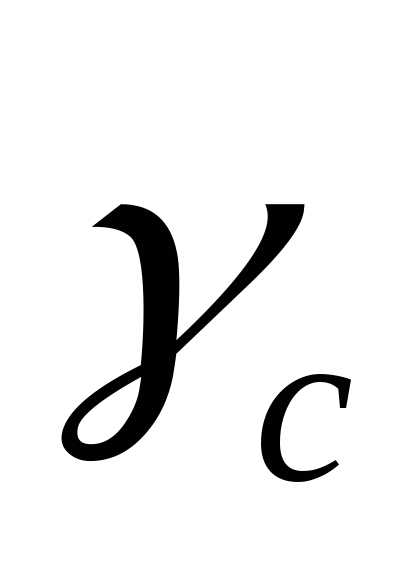 —
коэффициент условия работы.
—
коэффициент условия работы.
Производят проверку из условия жесткости по формуле
где  — относительный прогиб конструкций,
определяемый в результате расчета;
— относительный прогиб конструкций,
определяемый в результате расчета;
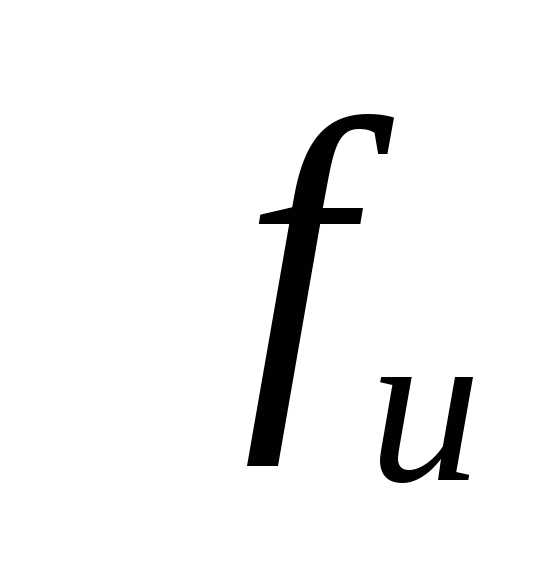 —
предельно допустимый относительный
прогиб, определяемый нормами
,
если
прогиб балки окажется более допустимого,
сечение балки следует увеличивать и
снова проверить жесткость балки.
—
предельно допустимый относительный
прогиб, определяемый нормами
,
если
прогиб балки окажется более допустимого,
сечение балки следует увеличивать и
снова проверить жесткость балки.
Расчет составных балок выполняют в следующей последовательности:
Определяют нагрузки и усилия (М и Q).
Определяют требуемый момент сопротивления

,
Оптимальная высота балки:

где =1,15…1,2 — конструктивный коэффициент сечения, предварительная толщина стенки , мм: ,
где h — высота балки, принимаемая равной 1/8…1/12 пролета балки, м.
Минимальная высота, обеспечивающая необходимую жёсткость:
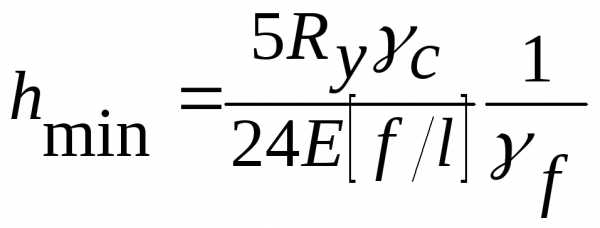 ,
,
где l — пролет балки;
Е=2,06х105 МПа — модуль упругости стали;
f/l — относительный прогиб балки согласно действующих норм.
Высота балки назначается близкой к hопт, но не менее hmin, принимается по сортаменту минус 10 мм на острожку кромок.
Принятая толщина стенки проверяется на срез:
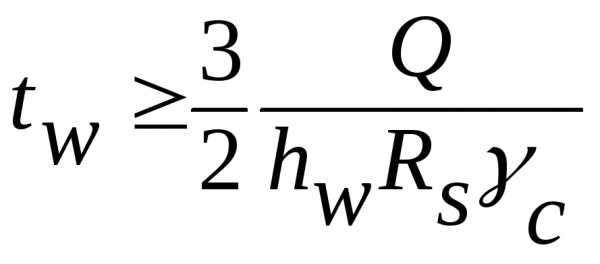 ,
,
где hw— высота стенки балки,
Rs=0,58Ry — расчётное сопротивление материала стенки срезу.
Требуемая площадь пояса:
,
где h=hw+2tf — предварительная высота балки.
Сечение поясов назначается с учетом требований общей и местной устойчивости. Ширина листа принимается bf /h=1/3…1/5, но не менее 180мм, а соотношения между шириной и толщиной пояса не должно превышать:
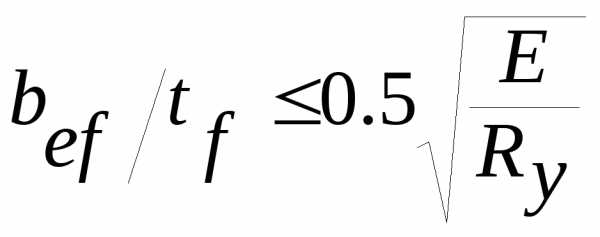
необходимую толщину определяют в оответствии с прокатываемыми толщинами. Толщина tf не должна бьпь менее tw и не более 2,5…3,0 толщины стенки.

Момент инерции сечения балки:
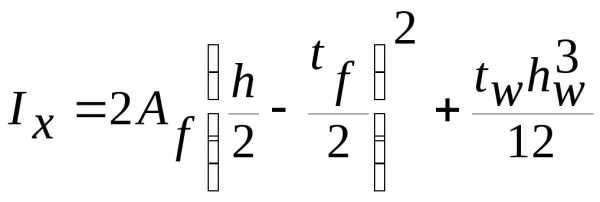
Напряжения в поясах от вертикальных нагрузок:

т.е. нормальные максимальные напряжения должны бьпь не более расчетного сопротивления стати по пределу текучести. Прогиб определяют методами строительной мехакники. Приведенный расчет достаточен при архитектурном проектировании. Детальный расчет включает нижеприведенные пункты.
Проверяют общую устойчивость балки.
Проверку не следует производить, если на балку опирается жесткий настил, и если соблюдается условие bf /l > 1/16, где l — расстояние между точками закрепления поясов балки.
Проверяют местную устойчивость элементов балки.
Местная
устойчивость сжатого верхнего пояса
обеспечена, если выполняется условие 
Местную устойчивость стенки необходимо проверять, если не выполняется условие
,
где hef=hw.
Расчёт на местную устойчивость стенки балки симметричного сечения выполняют в соответствии с требованиями раздела 7 СНиП II-23-81* по формуле:
 ,
,
Изменение сечениря по длине балки.
Для балок длиной 10…12 м необходимо менять сечение по длине (для экономии металла). Если изменять толщину пояса по длине балки, то уступы мешать настилу. Лучше менять ширину пояса. Изменять сечение удобнее всего на расстоянии 1/6 l (l — пролет балки) от опоры (рис.6.6.б).
Расчет опорного узла.
Опорный участок балок укрепляют рёбрами. Площадь опорного ребра:
 ,
,
где  — расчётное сопротивление смятию
торцевой поверхности при наличии
пригонки. При компоновке сечения ребраbp180мм,
— расчётное сопротивление смятию
торцевой поверхности при наличии
пригонки. При компоновке сечения ребраbp180мм, 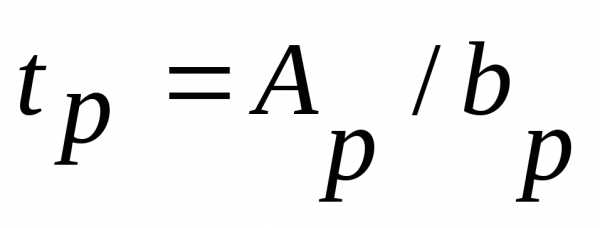 ,bp=bf.
,bp=bf.
Окончательные размеры опорного ребра определяют с учётом требований местной устойчивости:
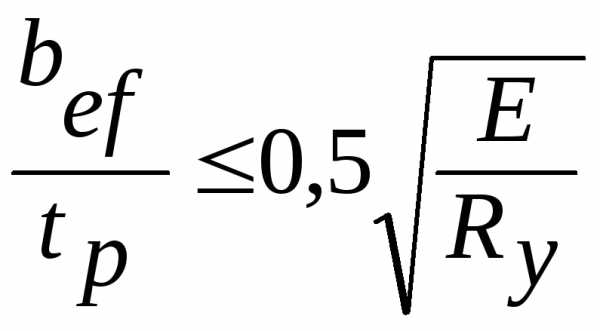
Условную опорную стойку, состоящую из ребра с частью стенки проверяют на устойчивость:
 ,
,
где,а коэффициент продольного изгиба зависит от гибкости:
Расчет поясных соединений
Поясные швы при подвижной нагрузке следует рассчитывать согласно СНиП II-23-81*
 ;
;
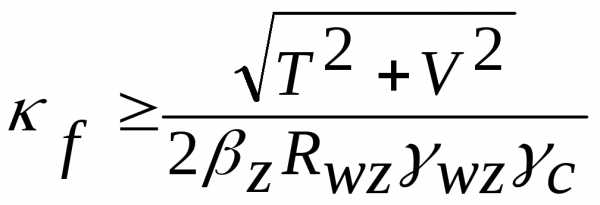 ,
,
где 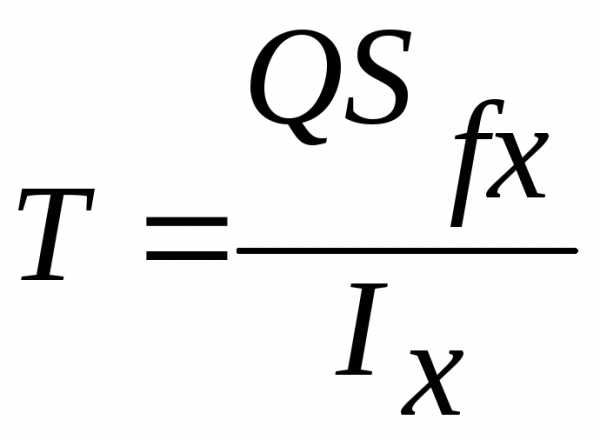 -сдвигающее
пояс усилие на единицу длины,
-сдвигающее
пояс усилие на единицу длины,
где 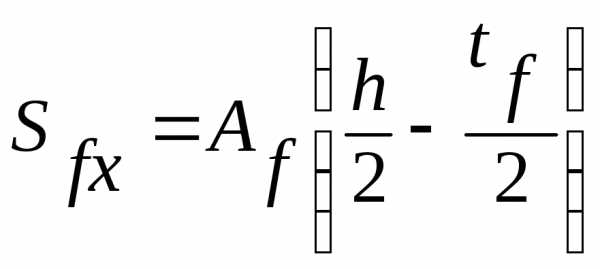 -статический
момент брутто пояса относительно
нейтральной оси;
-статический
момент брутто пояса относительно
нейтральной оси;
 — давление
от сосредоточенного груза F;
— давление
от сосредоточенного груза F;
f, z – коэффициент смотри раздел расчет сварных соединений.
Толщину шва принимают постоянной по всей длине балки.
studfile.net
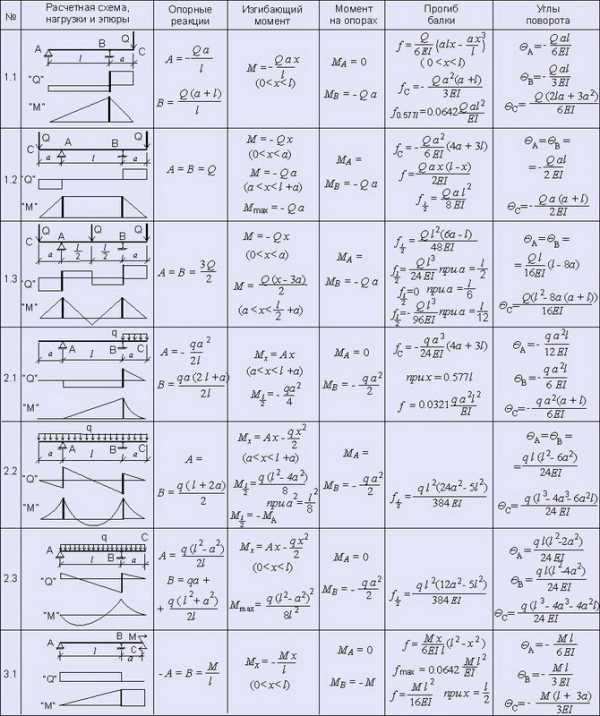
Представлены расчетные схемы, различные виды действующих нагрузок, эпюры сил, отображающие характер изменения касательных напряжений, эпюры изгибающих моментов, отображающие характер изменения нормальных напряжений, возникающих в поперечном сечении балки, а также формулы для определения опорных реакций, действующего изгибающего момента, максимального изгибающего момента, формулы для определения прогиба балки на расстоянии х от начала балки и формулы для определения максимального прогиба балки, а также формулы для определения тангенса угла поворота поперечного сечения на опорах и на концах — для консольных балок. Классификация производилась не по действующим нагрузкам, а по виду опор балки. В данном разделе представлены статически определимые балки. Ось х , относительно которой производятся расчеты изгибающего момента и прогиба, соответствует продольной оси, проходящей через центр тяжести поперечных сечений балки. Значение момента инерции I следует определять относительно оси z . Если в таблицах отсутствует формула для определения прогиба на каком-то из участков балки (из-за чрезмерной длины формулы), то опять же ее можно вывести, дважды должным образом проинтегрировав уравнение изгибающего момента, разделив результат на EI и добавив к этому результат интегрирования угла поворота. В общем виде уравнение для определения углов поворота выглядит так: θ х = — θ A + Мх/EI + Ax 2 /2EI — qx 3 /6ЕI например, для шарнирной балки, к которой приложена сосредоточенная нагрузка (таблица 1, №1.1, момент и распределенная нагрузка осутствуют) на участке от начала балки до точки приложения силы (0 θ х = — θ A + Ax 2 /2EI = — Ql 2 /16EI + Qx 2 /4EI = Q(4x 2 — l 2)/16EI Соответственно в общем виде уравнение для определения прогиба выглядит так: f х = — θ A x + Мх 2 /2EI + Ax 3 /6EI — qx 4 /24ЕI для той же шарнирной балки на участке от начала балки до точки приложения силы (0 f х = — θ A x + Ax 3 /6EI = — Ql 2 x/16EI + Qx 3 /12EI = Qx(4x 2 — 3l 2)/48EI На участке от точки приложения силы до конца балки (l/2 f х = — θ A x + Ax 3 /6EI — Q(x — l/2) 3 /6EI Эпюры углов поворота и прогибов поперечного сечения по длине балки не приводятся. Если в формуле прогиба есть знак минус, то это значит, что балка прогибается вниз (что в общем-то логично), а если быть более точным, то центр тяжести поперечного сечения смещается вниз по оси у . Представленные расчетные схемы позволяют рассчитать балку практически при любом возможном виде нагрузки. Если на балку действует несколько различных нагрузок, то можно производить отдельный расчет для каждой схемы загружения, а затем полученные результаты сложить (с учетом знаков). Это правило называется принципом суперпозиции и в некоторых случаях значительно упрощает общий расчет, а также экономит уйму времени на поиск в сети подходящей расчетной схемы. 1. БАЛКА НА ДВУХ ШАРНИРНЫХ ОПОРАХ 2. КОНСОЛЬНАЯ БАЛКА
3. БАЛКА НА ШАРНИРНЫХ ОПОРАХ С КОНСОЛЯМИ
Расчетные схемы для статически неопределимых балок . |
stroyew.ru