Балки перекрестные — Энциклопедия по машиностроению XXL

В течение 50—60-х гг. мировая практика накопила огромный опыт в развитии современных металлических конструкций. Были разработаны конструкции массового применения в виде традиционных балок, ферм и колонн для одноэтажных и многоэтажных промышленных и гражданских зданий, а также новые типы эффективных конструкций — предварительно напряженные фермы и балки, перекрестно-стержневые конструкции, вантовые и мембранные конструкции, сетчатые купола, своды и др.  [c.7]
I 9. Балки расположены перекрестно, как показано на рисунках.  [c.132]

Стальная балка швеллерного сечения № 8 длиной 3 м, сжатая силами Р, скреплена с двумя перекрестными балками тех же размеров. Сколько полуволн должно образоваться по потере устойчивости Определить критическую нагрузку пользуясь графиком, данным в решении задачи 8.

39.  [c.206]

Отсюда критическая нагрузка Р р = 2,3-3640 == 8350 кГ. Критическая жесткость опор соответствует значению с//Рэ = 81, Получае.м необходимый момент инерции перекрестной балки У, из уравнения  [c.390]

Типы металлических составных стержней показаны на рис. 1—3. На рис. 1 приведены наиболее употребительные типы металлических составных колонн. Для элементов, работающих на поперечный изгиб, характерны составные клепаные или сварные балки (рис. 2). Составляющими стержнями в них следует считать поясные листы, поясные уголки и стенку балки. К составным стержням можно отнести также растянутые или сжатые пакеты, стыкованные по длине внахлестку. Сюда относятся ступенчатые, универсальные и перекрестные клепаные стыки (рис. 3).  [c.5]

Перекрестная связь — связь, образуемая двумя перекрещивающимися балками, работающими на изгиб и подкрепляющими подвергаемый кручению пространственный каркас прямоугольного сечения.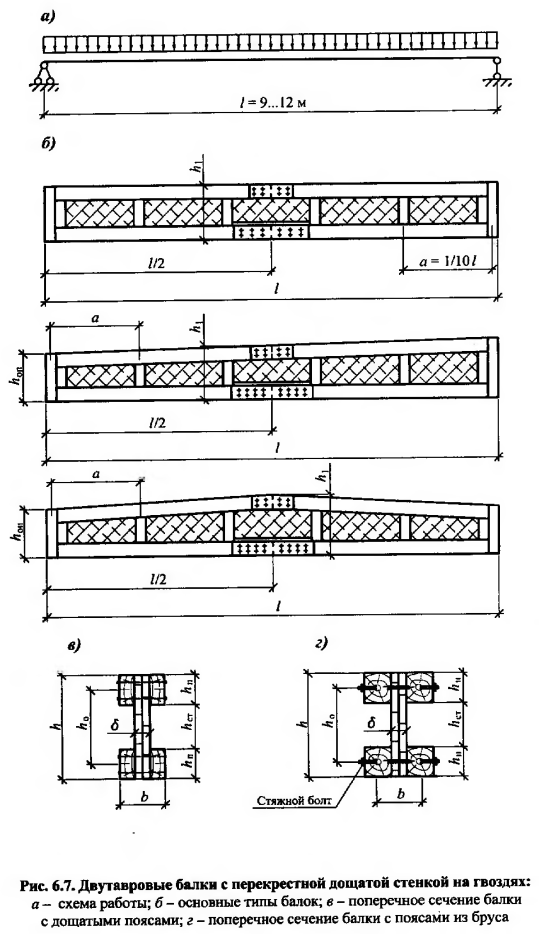

 [c.14]

Жесткость дополнительных крестообразных связей, показанных на рис. 7.4, можно оценить, если рассматривать крестообразную связь как две балки с заделанными концами, каждая из которых нагружает другую в середине длины пролета. Прогиб в середине-длины каждой перекрестной балки  [c.167]

Балки расположены перекрестно, как показано на рисунках, В местах пересечения балок при отсутствии нагрузки низ верхних балок касается верха нижних балок без нажима. Размеры балок обозначены на рисунке, причем  [c.240]

В качестве примера рассмотрим изгиб перекрестной балки АВ,  [c.192]

Через посредство обшивки на систему балочек передается равномерно распределенная нагрузка. Пусть Q — нагрузка, приходящаяся на одну балочку. Если бы балка А В была абсолютно жесткой и пересекала вертикальные балки посредине пролета, то давление от каждой из балочек, передаваемое перекрестной балке АВ, равнялось бы — -Q.

Вследствие прогиба перекрестной балки давление  [c.192]

Сосредоточенное давление R заменим сплошной нагрузкой, распределенной равномерно на протяжении d, равном расстоянию между вертикальными балочками. При значительном числе вертикальных балочек такая замена не произведет значительного влияния на прогиб балки Л 5, и мы можем с достаточной точностью считать, что на перекрестную балку АВ передается сплошная нагрузка, распределенная по закону  [c.192]

Увеличивая жесткость перекрестной балки, мы тем самым уменьшаем величину /С и, следовательно, увеличиваем давление R в  [c.193]

Если р обозначает число балок главного направления, г — число перекрестных балок, EJ[ — жесткость i-й балки главного направления и EJJ—жесткость /-й перекрестной балки, то потенциальная энергия изгиба нашей системы балок представится выражением  [c. 382]

Имея выражение для коэффициентов, легко найти прогиб любой перекрестной балки. Предположим, например, что у нас число перекрестных балок нечетное, и напишем уравнение изогнутой оси для средней балки, которой соответствует yr+i = lj2. Вставляя это  [c.384]

Наибольшую роль играет первый член этого выражения и обыкновенно в качестве первого приближения им можно ограничиться. Тогда можно сказать, что прогиб рассматриваемой перекрестной балки такой же, как у балки с опертыми концами, лежащей на сплош-  [c.384]

Мы до сих пор предполагали, что все перекрестные балки имеют одинаковую жесткость, такое же допущение мы делали и относительно балок главного направления, но тот же прием может быть с выгодой применен и в тех случаях, когда одной или нескольким балкам придано иное сечение. Ход решения задачи поясним на таком примере. Предположим, что плоское покрытие, несущее равномерную нагрузку, поддерживается одиннадцатью равноудаленными балками главного направления и пятью перекрестными балками. Концы всех балок предполагаются свободно поворачивающимися. Поперечные сечения всех балок главного направления одинаковы.  [c.385]

Имея значения коэффициентов а п, легко написать выражение для изогнутой оси каждой перекрестной балки.  [c.387]

Так, например, для средней перекрестной балки (i/=/i/2) получим  [c.387]

Величину изгибающего момента для каждой перекрестной балки найдем из формулы i)  [c.387]

Заметим, что при взятом нами числе знаков в выражениях для прогибов перекрестных балок третий знак в числах, полученных для моментов, является сомнительным. Конечно, можно было бы получить и более точные выражения для моментов, но такой расчет не имел бы практического значения, так как все решение задачи является по существу лишь приближенным. Мы, например, совершенно не принимали во внимание закона распределения давлений, получаемых балками главного направления от пластины плоского перекрытия, и приняли эти давления равномерно распределенными по плоскости покрытия. На самом деле этого нет, и получаемые вследствие этого погрешности будут в рассмотренном численном примере, вероятно, не меньше тех погрешностей, которые являются следствием неточного определения прогибов перекрестных балок. Выясненный на численном примере способ расчета перекрестных балок легко может быть распространен на тот случай, когда нагрузка неравномерная, а, например, меняется вдоль оси у по линейному закону. Если по концам перекрестных балок приложены моменты, то можно пользоваться тем же приемом расчета нужно только к работе нагрузки присоединить работу опорных пар.  

[c.388]

Здесь через 1 обозначен пролет и через Е/ — жесткость балок главного направления. Соответствующие величины для перекрестной балки обозначим через I ж Е1.  [c.199]

Перекрестная балка изгибается давлениями В, приложенными в местах пересечения ее с балками главного направления. Давления эти на основании (а) могут быть представлены так  [c.199]

Они имеют наименьшее значение в местах наибольшего прогиба перекрестной балки, т. е. у середины пролета АВ, 1 достигают наибольшей величины у концов перекрестной балки, где прогибы малы. Вычисление давлений Л, связанное с определением прогибов, мы выполним  

[c.199]

Таким образом, мы от изгиба сосредоточенными силами перейдем к изгибу сплошной нагрузкой, распределение которой вдоль перекрестной балки определяется ступенчатой линией (рис. 9). При большом числе балок главного направления мы можем заменить ступенчатую линию плавной кривой и таким образом свести расчет перекрестной балки к исследованию изгиба балки, нагруженной сплошной нагрузкой, изменяющейся по такому закону  [c.200]

Дифференциальное уравнение изогнутой оси перекрестной балки записывается так  [c.200]

Результатами последних двух параграфов воспользуемся при расчете перекрестных балок, с которыми приходится встречаться в строительной механике корабля и в некоторых гидротехнических сооружениях. Предположим, что требуется рассчитать плоское перекрытие с прямоугольным контуром, состоящее из пластины и подкрепляющих балок.

Нагрузка, воспринимаемая пла-стияой, передается системе равноудаленных балок, которые в дальнейшем будем называть балками главного направления. Эти балки поддерживаются опертой по концам перекрестной балкой АВ (рис. 8). Предположим, что все балки главного направления одинаково нагружены, оперты по концам и имеют одинаковое поперечное сечение. Возьмем одну из этих балок. Пусть Q обозначает ариходящуюся на эту балку сплошную нагрузку, передающуюся от пластины, и Л — реакцию, оказываемую на рассматриваемую балку перекрестной балкой АВ. Прогиб нашей балки в месте соприкасания ее с перекрестной балкой может быть представлен такой формулой  [c.199]

Две перекрестные балки длиной li и нагружены посе- редине силой Р. Найти распределение нагрузки между балками. Моменты инерции сечений балок соответственно Ji и У . Материал. балок одинаковый.  

[c.137]

Две перекрестные балки одинаковой длины / и равной жесткости EJ шарнирно оперты по концам, соединены ме вду собой лосередине. Одна из балок сжата силой Я, а вторая— силой kP,  [c.207]

Балки из композиционных материалов могут быть многослойные и трехслойные. Можно привести множество примеров многослойных балок от простого короткого образца для испытаний до более сложных двутавровых балок переменного сечения (рис. 15) или искривленных балок (рис. 16). Конфигурация трехслойных балок также может изменяться в пшроких (хотя и не до такой степени) пределах — от образца для испытаний (рис. 17) до перекрестных балок и панелей переменной толщины.  [c.133]

Сборная предварительно напряженная железобетонная оболочка положительной кривизны с размерами в плане 102×102 м построена в г. Челябинске [1]. Оболочка собрана пз ребристых панелей размером 298X1195 см, укладывающихся на перекрестную систему тавровых железобетонных балок (рис. 2.14). Панели по контуру окаймлены ребрами, высота которых у опорной зоны составляла 34 см, в середине пролета — 43 см. Кроме того, плита панелей толщиной 5 см подкреплена тремя поперечными ребрами.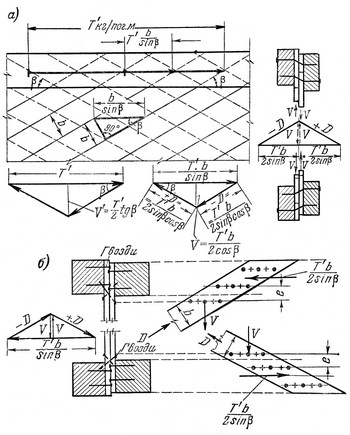

Балки длиной 1180 см, на которые укладывались плиты, имели переменную высоту 75 см у края, 88 см в середине пролета.  [c.73]

Работая над созданием барж с лучшими ходовыми качествами, устанавливая наивыгоднейшие основные размеры и находя рациональные очертания их остова, определяющие хорошую обтекаемость и максимальную грузоподъемность при малой осадке, В.Г. Шухов одновременно добивался конструктивной простоты. Поперечное сечение баржи, построенной в 1894 г. по заказу общества Меркульевы , представляет собой почти правильный прямоугольник. Две идущие вдоль баржи переборки из сплошного металлического листа создают три продольных отсека, которые в свою очередь разделяются рядом поперечных переборок. Переборки используются в качестве несущих диафрагм, и для придания им необходимой жесткости на них наклепаны стойки и перекрестные раскосы. Таким образом, Шухов создавал своеобразную кессонную систему из перекрещивающихся высоких продольных и поперечных балок со сплошными стенками. Внутренний отсек между двумя продольными переборками выполнен как жесткий ростверк, образуемый по дну продольными (кильсонными) и поперечными (шпангоут-ными) балками ). Каждая из металлических переборок, отделяющих друг от друга отсеки баржи, так же как и обшивка ее корпуса, играла не только роль конструктивно необходимого элемента. В.Г. Шухов умело использовал в расчете несущую способность этих элементов. получая, таким образом, значительную экономию в металле.  [c.128]

Частоты свободных колебаний открытой решетки (перекрытия) с большим числом одинаковых и равноотстоящих балок одного из направлений ( главное направлениел) и с несколькими перекрестными связями, одинаково установленными на опорах (рис. 13), совпадают с частотами изолированной балки главного направления, несущей сосредоточенные массы в точках пересечения с перекрестными балками, и опирающейся в этих точках на упругие опоры с жесткостью Кы (рис> 14). Прнчсм  [c.450]

В проектировании судов большое значение имеет теория плоских перекрытий из перекрестных продольных и поперечных балок, и Бубнов много сделал для разработки этой теории. Рассматривая систему параллельных равноотстоящих продольных балок, опирающихся на поперечную балку, Бубнов показал, что эту и тe -му можно трактовать как балку на упругом основании, и для проведения расчета именно по этому способу составил таблицы для  [c.525]

Предположим, что требуется рассчитать плоское перекрытие (рис. 1) с прямоугольным контуром, состоящее из тонкой пластины и подкрепляющих балок. Нагрузка, воспринимаемая пластиной, передается системе равноудаленных вертикальных балок, которые в дальнейщем бу- Л В дем называть балками главного направления. Эти балки поддерживаются несколькими горизонтально расположенными перекрестными балками. Расчет такой системы балок представляет задачу статически неопределимую с больщим числом лищних неизвестных.  [c.381]

Рассмотрим подробнее случай, когда балки главного направления равноудалены и имеют одинаковое поперечное сечение. Те же предположения сделаем относительно перекрестных балок и допустим, что система балок изгибается равномерно распределенной нагрузкой интенсивности q. Из условий симметрии можем заключить, что в общее выражение (3) для прогиба войдут лишь члены с нечетными значками m и п, и уравнения для определения коэффициентов Ujnn, получаемые из общего выражения (Ь), будут иметь такой вид 1=р  [c.383]

Здесь через Q обозначена величина qlil/(p+l), представляющая собой нагрузку, приходящуюся на одну балку главного направления. Множитель, стоящий перед скобками в полученном выражении для прогиба перекрестной балки, с достаточной точностью может быть принят равным прогибу балки главного направления при отсутствии перекрестных балок. Множителем 1—фо(ы) оценивается влияние перекрестных балок. На основании таблицы значений функции фо(ы) заключаем, что при я/2главного направления, но, наоборот, увеличивают ее прогиб. Когда прогибы перекрестных балок определены намеченным здесь способом, легко может быть рассчитана средняя балка главного направления. Для этого проще всего воспользоваться формулами для неразрезной балки с опорами, расположенными на различных высотах.  [c.385]

---

Определение перекрестных балок и ферм. Металлические и деревянные перекрестные балки и фермы; их основные параметры; узлы

— Перекрестные балки или фермы состоят из вертикальных пересекающихся в двух или трех направлениях ребер (балок или ферм).

— Особенности металлических перекрестных балок и ферм. Перекрестные балки двутаврового сечения имеют высоту h = l/24…l/30. Узлы пересечения конструируют так, чтобы разрыв полок компенсировали накладки, а разрыв стенки — сварные монтажные швы «втавр» (рис. 6.3, а). Накладки рассчитывают на продольное усилие N = М/h (где h — полная высота балки),а швы в стенке — на сдвигающее усилие Q, равное поперечной силе разрезанной балки в рассматриваемом узле. Металлические перекрестные фермы проектируют, как правило, с параллельными поясами, высотой примерно h = l/14. ..l/18. Перерезанные полки поясов компенсируют горизонтальными, а стенки — вертикальными фасонками.

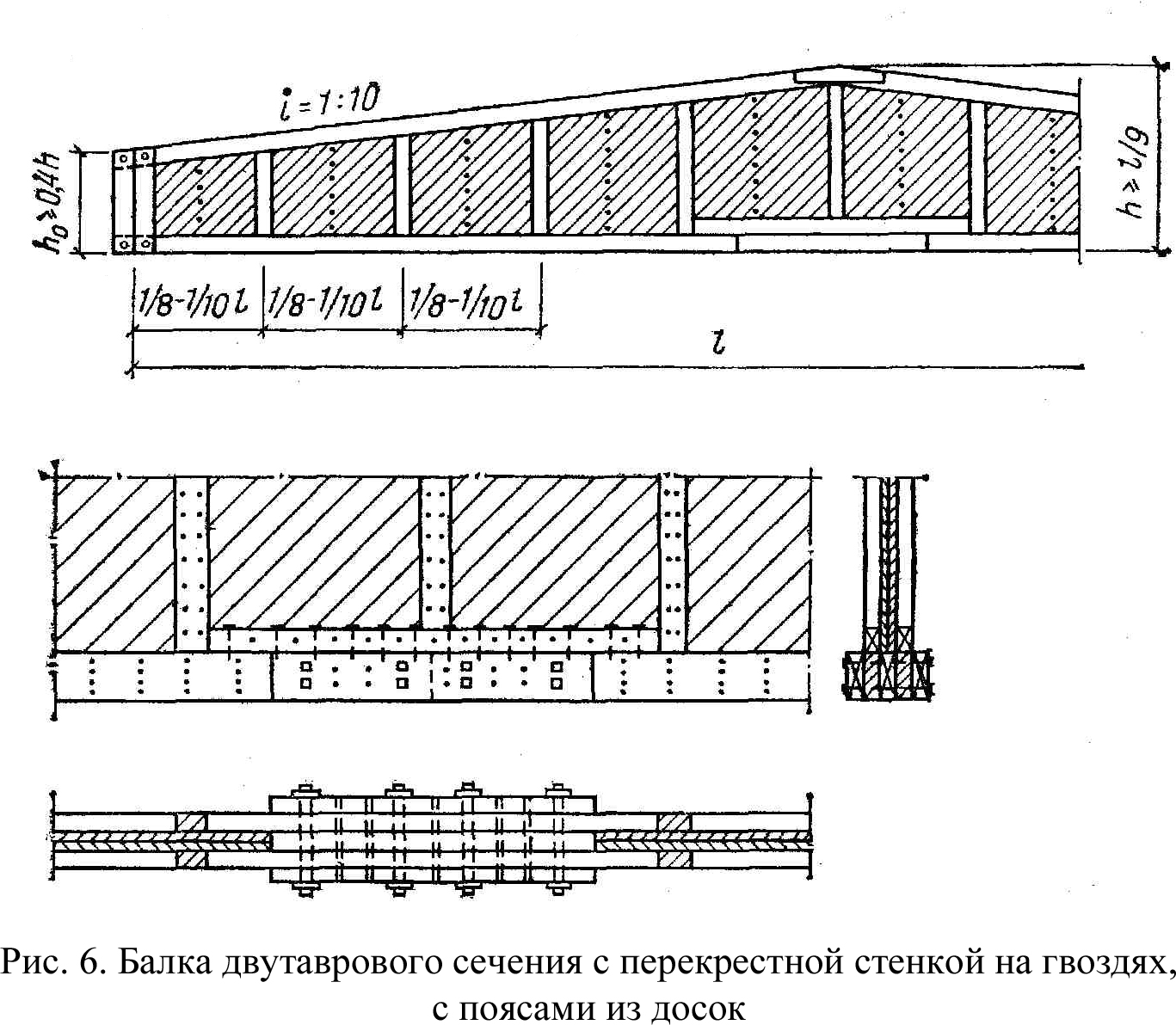
— Особенности деревянных перекрестных балок и ферм. Перекрестные балки в виде пакетов склеенных досок получили признание не только как рациональная конструкция, но и как выразительный элемент интерьера с глубоко кессонированным потолком. Перекрестными балками перекрывают пролеты от 1/2 до 24 м с шагом 3…6 м. Высоту балок назначают в пределах l/16..l/20.

Одно из решений узлов пересечения основано на перевязке слоев досок. К недостаткам этого узла относится необходимость выполнения склеивания непосредственно на монтажной площадке (построечное изготовление). Другие способы предусматривают использование металлических узловых деталей (рис. 6.4), которые рассчитывают на усилие N=M/h (где h — расстояние между центрами соединительных деталей). На это же усилие рассчитывают металлические элементы крепления (нагели, болты, глухари, гвозди, шпонки и др. ) к древесине.

12. Определение перекрестных балок и ферм. Основы расчета перекрестных балок и ферм.

Перекрестные балки или фермы состоят из вертикальных пересекающихся в двух или трех направлениях ребер (балок или ферм).

Формулы для расчета перекрестных балок на квадратном плане, расположенных параллельно сторонам или диагоналям:

Методика подбора сечений перекрестных балок и ферм не имеет принципиальных отличий от методики расчета обычных балок и ферм. Для ориентировки следует иметь в виду, что эквивалентная нагрузка на перекрестные балки и максимальные изгибающие моменты составляют примерно 50…60% от аналогичных величин для простых балок. Следовательно, высота перекрестных балок может составлять около 0.7…0,8 высоты простых балок, а высота перекрестных ферм — 0,6…0,7 ,высоты обычных ферм.

13. Определение структурных конструкций. Этапы их развития. Основной закон построения структур.

    Область применения; достоинства и недостатки.

— Структурами обычно называют системы стержней, сходящихся в узлах и расположенных в пространстве в строгом геометрическом порядке. В Советском Союз, бурное развитие структур положено постановлением ЦК КПСС и Совета Министров СССР от 29 мая 1972 г. Серийно изготовляются структурные конструкции из прокатных профилей системы «ЦНИИСК» и труб системы «МАрхИ» и «Кисловодск».

Решетчатые плиты (структурные покрытия) получили широкое распространение в качестве плоских покрытий с пролетами до 100 м.

— Этапы развития структуры. Для структур, образованных стержнями одинаковой длины, возможности «скульптурного» метода построения (из структурно организованного пространства выделяют требуемую форму и отсекают лишнее) ограничены неизменностью углов а наклона к горизонту граней структурной конструкции, «атомами» которой служат полуоктаэдры и тетраэдры (схема 1/2 (0 + Т). Композиционные возможности формообразования пространственных структурных конструкций значительно расширяются с введением дополнительного размера стержней а√2. Узловой элемент в этом случае должен обладать способностью присоединения 18 стержней. При этом образуются не только новые углы, но и появляется возможность перехода от одной системы стержней к другой без нарушения единства структуры. Дальнейшее развитие форм структурных конструкций может идти по линии использования стержней трех типоразмеров: а, а√2 и а√3. Узловой элемент такой системы должен обладать способностью принять стержни 26 направлений.

— Структурное покрытие является прежде всего стержневой (решетчатой) плитой и поэтому основные принципы проектирования сплошных плит справедливы н для них:

1. Наиболее выгодной формой прямоугольных плит является квадратная.

2. Чем чаще расположены опоры по контуру плиты, тем лучше, хотя польза от слишком частого их расположения становится незаметной. В наихудших условиях работает плита, опертая по- углам (а) или в серединах сторон со свисающими углами (6).

3. Эффективен конструктивный прием постановки опор с некоторым отступом от контура покрытия (д). Образующиеся консольные свесы способствуют снижению величин изгибающих моментов в пролете, причем создается самостоятельный планировочный модуль, легко поддающийся блокировке с другими подобными модулями.

— Область применения: промышленное и гражданское строительство, применение в сейсмических районах.

— Достоинства структурных покрытий: пространственная работа при многократной статической неопределимости (многосвязности системы), гарантирующая перераспределение усилий в стержнях при внезапном разрушений некоторых из них; однотипность узлов и стержней; примерно двукратное по сравнению с плоскими фермами снижение строительной высоты конструкции; облегчение кровельного покрытия и подвесных потолков благодаря частому расположению опорных точек в узлах; легкая приспособляемость к планам сложным и с нерегулярной расстановкой опор; выразительность в интерьере и при выносе конструкций на фасад.

Недостатками структурных покрытий, порой диалектически сопряженными с их достоинствами, являются: сложность узлов и высокая требуемая точность их изготовления; неизбежные «люфты» в многочисленных соединениях (исключая сварные).

Справочник проектировщика промышленных, жилых и общественных зданий и сооружений. Расчетно-теоретический. 1960 г. Уманский А.А.

РАЗДЕЛ 1. МАТЕМАТИКА. Чл.-корр. АН УССР д-р физ.-мат. наук проф. И. Я. Штаерман 19
1.1. Алгебра 19
1.1.1. Степени и корни 19
1.1.2. Логарифмы 19
1.1.3. Прогрессии 20
1.1.4. Факториал 20
1.1.5. Соединения 20
1.1.6. Бином Ньютона 20
1.1.7. Определители (детерминанты) 20
1.1.8. Линейные уравнения 21
1.1.9. Матрицы (канд. техн. наук В. В. Новицкий) 22
1.1.10. Уравнения высших степеней 23
1.1.11. Приближенное решение уравнений 24
1.2. Геометрия 25
1.2.1. Плоские фигуры. Многоугольники .Круг и его части. Площади, ограниченные кривыми второго порядка 25
1.2.2. Тела. Тела, ограниченные плоскостями. Цилиндр и конус. Шар и его части. Некоторые другие тела. Тела вращения (теоремы Гюльдена). Призматоид. Рампа 26
1.3. Тригонометрия 27
1.3.1. Измерение углов 27
1.3.2. Тригонометрические (круговые) функции . . 27
1.3.3. Функции суммы и разности углов, кратных углов и половинного угла 29
1.3.4. Степени функций 29
1.3.5. Приведение к виду, удобному для логарифмирования 29
1.3.6. Зависимости между функциями трех углов, сумма которых равна 180° 29
1.3.7. Зависимости между обратными тригонометрическими функциями 30
1.3.8. Формулы, применяемые при решении треугольников 30
1.3.9. Гиперболические функции 31
1.4. Аналитическая геометрия 31
1.4.1. Точка на плоскости 31
1.4.2. Прямая линия 32
1.4.3. Окружность 32
1.4.4 Парабола 32
1.4.5. Эллипс и гипербола 33
1.4.6. Построение конических сечений 34
1.4.7. Цепная линия. Циклоида. Спираль 34
1.4.8. Точка в пространстве 34
1.4.9. Плоскость 35
1.4.10. Прямая в пространстве 35
1.4.11. Поверхности второго порядка 35
1.5. Дифференциальная геометрия 36
1.5.1. Плоские кривые 36
1.5.2. Пространственные кривые 38
1.5.3. Поверхности 39
1.6. Дифференциальное исчисление 39
1.6.1. Функция, предел, непрерывность 39
1.6.2. Производная и дифференциал 40
1.6.3. Раскрытие неопределенностей 41
1.6.4. Исследование функций 41
1.6.5. Функция двух переменных 41
1.7. Интегральное исчисление 42
1.7.1. Неопределенный интеграл 42
1.7.2. Интегрирование рациональных функций 43
1.7.3. Интегрирование иррациональных функций 44
1.7.4. Интегрирование трансцендентных функций 44
1.7.5. Определенный интеграл 46
1.7.6. Кратные интегралы 47
1.7.7. Криволинейные интегралы 48
1.8. Ряды 48
1.8.1. Числовые ряды 48
1.8.2. Степенные ряды 49
1.9. Дифференциальные уравнения 51
1.9.1. Основные понятия 51
1.9.2. Уравнения первого порядка 51
1.9.3. Уравнения второго порядка 51
1.9.4. Линейные уравнения второго порядка 52
1.9.5. Линейные уравнения высших порядков с постоянными коэффициентами 53
1.9.6. Метод начальных параметров 53
1.9.7. Общие решения дифференциального уравнения четвертого порядка с биквадратным характеристическим уравнением (канд. техн. наук А. И. Тюленев) 54
1.9.8. Приближенные методы 54
1.9.9. Уравнения математической физики 58
1.9.10. Квазилинейные уравнения 59
1.10. Функции комплексной переменной 60
1.10.1. Комплексные числа 60
1.10.2. Комплексные функции 60
1.10.3. Конформные отображения 61
1.11. Вариационное исчисление 61
1.11.1. Постановка задачи 61
1.11.2. Основные случаи 62
1.11.3. Прямые методы 63
1.12. Разностное исчисление 63
1.12.1 Определение разностей 63
1.12.2. Разностные уравнения 63
1.13. Интегральные уравнения 64
1.13.1. Уравнения Фредгольма. Методы решения однородного уравнения. Методы решения неоднородного уравнения 64
1.13.2. Уравнения Вольтерра второго рода 65
1.13.3. Уравнения Абеля 65
1.13.4. Сингулярные уравнения 65
1.14. Специальные функции 66
1.14.1. Полиномы Лежандра 66
1.14.2. Полиномы Чебышева 66
1.14.3. Гамма-функция 66
1.14.4 Функции Бесселя 66
1.15. Операционное исчисление 67
1.15.1. Преобразование Лапласа 67
1.15.2. Применение операционного исчисления 68
1.16. Векторное и тензорное исчисления 68
1.16.1. Векторная алгебра 68
1.16.2. Векторный анализ 69
1.16.3. Тензоры 69
1.17. Приближенные вычисления 70
1.17.1. Общие положения 70
1.17.2. Приближенные формулы 71
1.18. Номография 71
1.18.1. Функциональная шкала 71
1.18.2. Номограммы из выравненных точек 71
1.18.3. Сетчатые номограммы 72
1.18.4. Номограммы для уравнений с числом переменных более трех 72
1.19. Приближенное представление функций 72
1.19.1. Постановка задачи 72
1.19.2. Интерполяционные формулы 72
1.19.3. Приближение функций по методу наименьших квадратов 74
1.19.4. Приближенное вычисление определенных интегралов 75
1.20. Ряды Фурье 76
1.20.1. Разложение функций в ряд Фурье 76
1.20.2. Интеграл Фурье 79
1.20.3. Приближенный гармонический анализ 80
1.21. Теория вероятностей 81
1.21.1. Понятие вероятности 81
1.21.2. Случайные величины 82
1.21.3. Обработка наблюдений 82
1.21.4. Основы теории корреляции 83
1.22. Математические таблицы 84
1.22.1. Степени, корни, натуральные логарифмы 84
1.22.2. Тригонометрические функции. Синусы и косинусы 92
1.22.3 Круговые, показательные и гиперболические функции 94
1.22.4. Некоторые постоянные 97
1.22.5. Соотношение между английскими и метрическими мерами 97
РАЗДЕЛ 2. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. Д-р техн. наук проф. А. Н. Обморшев. 99
СТАТИКА 99
2.1. Геометрическая статика 99
2.1.1. Основные положения 99
2.1.2. Сложение и разложение сил 100
2.1.3. Моменты сил и пар 100
2.1.4. Параллельные силы 101
2.1.5. Произвольная система сил 101
2.1.6. Правила прикрепления твердого тела 104
2.1.7. Системы с трением 104
2.1.8. Центр тяжести 105
2.2. Графостатика 106
2.2.1. Веревочный многоугольник 106
2.2.2. Применение веревочного многоугольника к определению опорных реакций 108
2.2.3. Определение усилий в стержнях плоских статически определимых ферм 109
2.2.4. Разложение силы по трем прямым, пересекающимся в одной точке и не лежащим в одной плоскости 110
2.2.5. Разложение силы по шести произвольно расположенным прямым 110
2.3. Аналитическая статика 111
2.3.1. Работа. Мощность 111
2.3.2 Потенциальная энергия 112
2.3.3. Принцип возможных перемещений 113
КИНЕМАТИКА 113
2.4. Кинематика точки 113
2.4.1 Прямолинейное движение точки 113
2.4.2. Криволинейное движение точки 114
2.4.3. Относительное движение точки 115
2.5. Кинематика твердого тела 115
2.5.1. Поступательное движение 115
2.5.2. Вращение вокруг неподвижной оси 115
2.5.3. Винтовое движение 116
2.5.4. Плоско-параллельное движение 116
2.5.5. Движение тела около неподвижной точки 117
2.5.6. Сложение скоростей или бесконечно малых перемещений при сложном движении твердого тела. Статико-кинематическая аналогия 117
2.5.7. Элементы кинематики механизмов 118
2.5.8. Кинематические пары, входящие в расчетные схемы сооружений 118
ДИНАМИКА 120
2.6. Механические единицы 120
2.6.1. Правило размерностей 120
2.7. Динамика точки 121
2.7.1. Основные законы 121
2.7.2. Прямолинейное движение точки 121
2.7.3. Криволинейное движение точки 122
2.7.4. Кинетостатика точки. Относительное движение 122
2.8. Динамика системы 122
2.8.1. Общие теоремы динамики 122
2.8.2. Общие принципы динамики системы 123
2.8.3. Моменты инерции 124
2.9. Динамика твердого тела 125
2.9.1. Вращение тела вокруг неподвижной оси 125
2.9.2. Физический маятник 125
2.9.3. Давление вращающегося тела на опоры 126
2.9.4. Плоско-параллельное движение 126
2.10. Удар 126
2.10.1. Основные положения 126
2.10.2. Удар двух тел 126
2.10.3. Действие удара на вращающееся твердое тело 127
РАЗДЕЛ 3. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ. Д-р техн. наук И. И. Трапезин 129
3.1. Напряжения 129
3.1.1. Основные понятия 129
3.1.2. Одноосное напряженное состояние 129
3.1.3. Плоское напряженное состояние 130
3.1.4. Объемное напряженное состояние 130
3.1.5. Преобразование компонентов напряжения к новым осям координат 132
3.1.6. Интенсивность напряжений в данной точке 132
3.1.7. Круги Мора 133
3.2. Деформации 134
3.2.1. Компоненты деформаций 134
3.2.2. Определение угловой деформации и величин главных удлинений по удлинениям в трех направлениях в случае плоской деформации и плоского напряженного состояния 135
3.2.3. Интенсивность деформаций 135
3.3. Зависимости между напряжениями и деформациями в пределах упругости 136
3.3.1. Закон Гука для изотропного тела 136
3.3.2. Закон Гука для анизотропного тела 137
3.3.3. Плоскость симметрии в отношении упругих свойств 137
3.3.4. Ортотропное упругое тело 137
3.3.5. Потенциальная энергия упругого тела 138
3.4. Связь между напряжениями и деформациями за пределами упругости 138
3.4.1 Условия пластичности 138
3.4.2 Напряжения и деформации при простом нагружении и при разгрузке 138
3.4.3 Диаграммы растяжения 139
3.4.4 Схематизация истинных диаграмм растяжения 139
3.4.5. Построение кривой зависимости 140
РАЗДЕЛ 4. ПРОЧНОСТЬ МАТЕРИАЛОВ И МЕТОДЫ РАСЧЕТА КОНСТРУКЦИЙ. Кандидаты техн. наук доценты А. И. Коданев, В. Г.Чернашкин, Б. А. Дзержкович, чл.-корр. АСиА СССР канд. техн. наук С. А. Семенцов, канд. техн. наук Л. Н. Пицкель, д-р техн. наук проф. В. Н. Быковский, д-р техн. наук А. Б. Губенко, кандидаты техн. наук А. Г. Иммерман, Л В. Клепиков, В. А. Отставнов 141
4.1. Прочность материалов (А. И. Коданев) 141
4.1.1. Упругость, пластичность и разрушение 141
4.1.2. Влияние характера напряженного состояния 141
4.1.3. Влияние температуры 144
4.1.4. Влияние длительности нагружения 144
4.1.5. Влияние переменности нагрузки 145
4.1.6. Влияние концентрации напряжений 147
4.1.7. Влияние скорости приложения нагрузки 147
4.2. Строительные стали (В. Г. Чернашкин) 148
4.2.1. Основные понятия и обозначения 148
4.2.2. Физические свойства углеродистой стали 148
4.2.3. Химический состав и механические свойства углеродистой стали. Сталь углеродистая горячекатаная обыкновенного качества пс ГОСТ 380-50. Сталь углеродистая для мостостроения. Сталь углеродистая для армирования железобетонных конструкций 149
4.2.4. Химический состав и механические свойства низколегированной стали. Сталь низколегированная 10ХНДП (СХЛФ) с повышенным содержанием фосфора. Сталь низколегированная марки 10Г2СД (МК). Сталь низколегированная марок 14ХГС и 19Г. Сталь низколегированная марки 15ГС 156
4.3. Сплавы алюминия для строительства(Б. А. Дзержкович) 162
4.4. Бетон (С. А. Семенцов) 164
4.4.1. Прочность 164
4.4.2 Деформация 166
4.5. Каменные материалы (С. А. Семенцов) 171
4.5.1. Прочность 171
4.5.2 Деформации 173
4.6. Армированные материалы (Л. Н. Пицкель) 174
4.6.1. Общие сведения 174
4.6.2. Железобетон 175
4.6.3. Армоцемент 179
4.6.4. Армированные каменные конструкции 179
4.6.5. Армированный асбестоцемент 180
4.7. Древесина (В. Н. Быковский) 181
4.7.1. Общие сведения 181
4.7.2. Механические свойства 181
4.8 Пластмассы в строительных конструкциях (А. Б. Губенко) 183
4.8.1. Конструктивные пластмассы 183
4.8.2. Конструкции с применением пластмасс 185
4.8.3. Клеи и склеивание конструкций с применением пластмасс 186
4.9 Методы расчета конструкций 186
4.9.1. Метод расчета по расчетным предельным состояниям (Л. В. Клепиков, В. А. Отставнов) 186
4.9.2. Метод расчета по разрушающим нагрузкам (А. Г. Иммерман) 191
4.9.3. Метод расчета по допускаемым напряжениям (А. Г. Иммерман) 192
РАЗДЕЛ 5. СТРОИТЕЛЬНАЯ МЕХАНИКА БРУСА И СИСТЕМ БРУСЬЕВ. Д-р техн. наук проф. А. А. Уманский 195
5.1. Основные положения технической теории бруса 195
5.1.1. Определения 195
5.1.2. Основные факторы работы бруса. Статико-кинематическая аналогия. Нагрузки и усилия. Деформации и перемещения. Статико-кинематическая аналогия 195
5.1.3. Интегральные соотношения между напряжениями и усилиями в поперечных сечениях 197
5.1.4. Соответствующие силы и перемещения, усилия и дислокации 197
5.1.5. Начальная, температурная и упругая распределенные деформации 199
5.1.6. Две системы координатных осей упругого бруса с несимметричным сечением 200
5.1.7. Упругое основание 200
5.1.8. Плоский неразветвленный упругий брус. Обобщенная статико-кинематическая аналогия 200
5.2. Определение нормальных напряжений 202
5.2.1. Геометрические характеристики поперечных сечений брусьев 202
5.2.2. Определение моментов инерции относительно исходных осей 203
5.2.3. Редуцирование площадей при вычислении моментов инерции 203
5.2.4. Общая формула нормального напряжения при растяжении-сжатии и изгибе. Нейтральная линия 205
5.2.5. Максимальные нормальные напряжения 206
5.2.6. Ядро сечения 206
5.2.7. Случай переменного модуля Е 207
5.2.8. Пользование центральными неглавными осями 207
5.3. Определение касательных напряжений и деформаций в брусьях. Особенности тонкостенных сечений 208
5.3.1. Расчет на срез (сдвиг) 208
5.3.2. Расчет на направленный срез (сдвиг). Формулы для погонных касательных усилий и напряжений 208
5.3.3. Касательные напряжения при изгибе. Центр изгиба 210
5.3.4. Деформация сдвига при изгибе брусьев с массивным сечением и двутавровых балок 212
5.3.5. Касательные напряжения при изгибе и центр изгиба открытых тонкостенных сечений 212
5.3.6. Касательные напряжения при изгибе и центр изгиба замкнутых тонкостенных сечений 215
5.3.7. Касательные напряжения и относительный угол закручивания при свободном кручении. Геометрические характеристики 217
5.3.8. Депланация при свободном кручении. Эпюры единичной депланаций при свободном кручении для тонкостенных сечений 219
5.3.9. Стесненное кручение 219
5.3.10. Сложное сопротивление тонкостенных брусьев. Приведение нагрузок к типам усилий 221
5.4. Классификация систем брусьев и общие методы строительной механики 222
5.4.1. Основные определения 222
5.4.2. Виды систем Балки. Арки. Рамы. Фермы. Комбинированные системы. Спаренные плоские системы (биконструкции) 223
5.4.3. Статический метод определения перемещений и кинематический метод определения усилий на примере балки. Инфлюенты (линии и поверхности влияния). Статический метод определения перемещения в статически определимой системе. Кинематический метод определения усилия в статически определимой системе. Обобщенная теорема о взаимности работ активных факторов, действующих на упругую систему. Формулы для перемещения в упругой с. н. системе. Формулы для усилия в с. н. системе. Теоремы о взаимности единичных перемещений и усилий 226
5.4.4 Метод потенциальной энергии. Выражение энергии деформации через обобщенные силы и обобщенные перемещения. Выражение энергии деформации через силы и единичные перемещения. Выражение энергии деформации системы брусьев через усилия. Теорема Кастильяно. Теорема о минимуме энергии деформации. Случай заданных (температурных или начальных) деформаций. Выражение энергии деформации через перемещения или дислокации. Теорема об экстремуме полной энергии. Случай нелинейно-деформируемой системы, когда энергия деформации не есть функция второй степени от нагрузок 229
5.5. Балки 231
5.5.1. Определение усилий и перемещений и построение эпюр в балках по методу начальных параметров. Общие положения. Обыкновенная балка постоянного сечения. Обыкновенная балка переменного сечения . «Графоаналитический» метод определения перемещений в обыкновенных балках. Концевые углы поворота сечений простой балки как фиктивные реакции 231
5.5.2. Абсолютно жесткая балка на упругом основании и обыкновенная балка с защемленными концами. Уравнения эпюр. Абсолютно жесткие балки со свободными концами на упругом основании. Обыкновенные балки с защемленными концами 238
5.5.3. Приемы, упрощающие построение эпюр и инфлюент статически определимых балок 240
5.5.4. Равнопролетные неразрезные балки на жестких опорах. Метод бесконечной основной системы. Полубесконечная балка. Бесконечная балка. Построение инфлюент. Конечная равнопролетная балка 241
5.5.5. Равнопролетные неразрезные балки постоянного сечения на упруго оседающих опорах. Метод начальных параметров. Бесконечная и полубесконечная балки. Расчет конечных равнопролетных балок по таблицам для бесконечных балок 243
5.5.6. Балка на упругом (винклеровском) основании. Общие данные. Уравнения эпюр. Однопролетная балка. Бесконечная двусторонняя балка. Полубесконечная балка. Использование бесконечной балки для расчета конечных балок (Метод компенсирующих нагрузок). Практические указания. Дополнительная литература 248
5.5.7. Общий метод расчета неразрезных балок на жестких опорах. Уравнение трех опорных моментов 253
5.5.8. Решение системы уравнений трех моментов и общих трехчленных уравнений. Аналитический способ. Графический способ. Определение чисел влияния. Построение инфлюент усилий Qu и Мu в промежуточных сечениях неразрезной балки и инфлюент реакций Vn 255
5.5.9. Неразрезная балка на упруго оседающих опорах. Уравнение пяти опорных моментов 262
5.6. Арки и простые рамы 263
5.6.1. Общие положения 263
5.6.2. Трехшарнирная арка. Реакции и усилия при постоянной нагрузке. Инфлюенты (линии влияния). Эпюры углов поворота и прогибов арки 263
5.6.3. Статически неопределимые арки. Универсальные формулы для усилий. Характеристики фиктивного профиля. Определение факторов Рф, Lx, Ly. Определение опорных моментов и опорных реакций. Инфлюенты усилий в бесшарнирной арке. Использование общих формул для расчета одно- и двухшарнирной арок. Упруго защемленная арка 266
5.6.4. Двухшарнирная арка. 269
5.6.5. Упрощенный расчет двухшарнирных и бесшарнирных параболических арок. Учет обжатия 270
5.6.6. Одноконтурные (простые) рамы. Статически определимые рамы. Статически неопределимые рамы. Упрощения в расчете геометрических характеристик гибкости и фиктивных нагрузок 272
5.6.7. Бесшарнирные арки и рамы под нагрузкой, перпендикулярной их плоскости 275
5.7. Сложные рамы 276
5.7.1. Классификация методов 276
5.7.2. Расчет рам по способу трех и четырех моментов. Закрепленная эстакада. Свободная эстакада. Простая балка переменного сечения как элемент основной системы. Ступенчатая стойка. Ломаная или криволинейная балка. Уравнение трех моментов для неразрезной балки с пролетами в виде параболических арок с затяжками. Зависимости между перемещениями и уравнения равновесия в сложных случаях 277
5.7.3. Метод перемещений. Общие положения. Формулы для усилий (реакций) защемлений от местной нагрузки или заданной деформации и перемещений торцов. Составление уравнений из условий равновесия. Стандартные формулы для составления уравнений метода перемещений. Канонические уравнения метода перемещений для свободной рамной эстакады 281
6.7.4. Метод сил. Общие положения. Выбор основной системы, составление и решение канонических уравнений. Специальные приемы упрощения и контроля расчета по методу сил. Дополнительная литература 287
5.8 Расчет рам методом последовательных приближений 291
5.8.1. Способ распределения моментов (инженеры А. Н. Газарян и Я. К. Канонов) . Несвободные рамы. Свободные рамы. Многоярусные рамы. Дополнительная литература 291
5.8.2. Способ распределения углов поворота (канд. техн. наук П. М. Сосис) 296
5.8.3. Расчет многоэтажных рам на горизонтальную нагрузку (канд. техн наук доц. Я. Б. Львин). Однопролетная рама. Применение однопролетной схемы к расчету многопролетных рам 298
5.8.4. Метод фокусов (фокусных отношений). Общие положения. Формулы и приемы метода моментных фокусов. Формулы метода угловых фокусов. Область применения метода фокусов 300
5.9. Расчет пространственных рам с взаимно перпендикулярными брусьями по методу перемещений 304
5.9.1. Основные зависимости и формулы 304
5.9.2. Пример 306
5.10. Тонкостенные брусья 307
5.10.1. Прямые тонкостенные брусья с жестким поперечным сечением и пренебрежимо малой жесткостью свободного кручения 307
5.10.2. Тонкостенные брусья с жестким поперечным сечением и конечной жесткостью свободного кручения 309
5.10.3. Кривые тонкостенные брусья и арки с жестким поперечным сечением 311
5.10.4. Рамы из тонкостенных брусьев и бирамы 312
5.10.5. Поперечные изгибающие моменты и учет деформации контура поперечного сечения в тонкостенных брусьях 312
5.10.6. Приближенный расчет тонкостенных брусьев и цилиндрических оболочек с открытым деформируемым поперечным сечением (д-р техн. наук проф. С. Н. Кан и канд. техн. наук доц. П. А. Школьный) 313
5.11. Специальные вопросы 316
5.11.1. Конструкции типа составных брусьев. Многоэтажные рамы под горизонтальной нагрузкой. Каркасно панельные стены. Составная балка с пенсами, работающими на изгиб, и стенкой, работающей на сдвиг. Многопоясные составные брусья 316
5.11.2. Комбинированные и предварительно напряженные конструкции. Комбинированные конструкции. Предварительно напряженные металлические балки 321
5.11.3. Гибкие нити. Общие положения. Провисание непологой нити под действием собственного веса. Пологая нить (канд. техн. наук Р. Н. Мацелинский). Примеры расчета (Р. Н. Мацелинский). Стальные канаты. Дополнительная литература 323
5.11.4. Пневматические конструкции (доц. В. Н. Архангельский и инж А. Н Глухарев). Определения и основные сведения. Особенности расчета ПК. Расчет оболочки, работающей на избыточное давление. Расчет аэробалки. Определение деформаций ПК. Материалы для ПК. Литература 329
РАЗДЕЛ 6. РЕШЕНИЕ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ. Действ, член АСиА СССР д-р техн. наук проф.Б. Н. Жемочкин, д-р техн. наук проф.А. А. Уманский 339
6.1. Способ Гаусса 339
6.1.1. Схемы вычислений 339
6.1.2. Примеры 341
6.1.3. Решение трехчленных уравнений 344
6.1.4. Числа влияния и их определение по способу Гаусса 344
6.2. Способ последовательных приближений (способ итерации) 345
6.3. Решение уравнений с помощью настольных вычислительных машин (инженеры К. П. Вишневский и Б. Л. Тарнопольский) 348
6.3.1. Компактные схемы способа Гаусса 348
6.3.2. Метод квадратных корней 351
6.4. Механизация решений уравнений 351
РАЗДЕЛ 7. ТАБЛИЦЫ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК СЕЧЕНИЙ БРУСЬЕВ. Канд. техн. наук доц. В. В. Новицкий 353
7.1. Геометрические характеристики при растяжении-сжатии и изгибе 353
7.2. Приближенные значения радиусов инерции 362
7.3. Положение центра изгиба некоторых сечений 363
7.4. Геометрические характеристики при свободном кручении 365
7.5. Положение центра изгиба и бимоменты инерции сечений составных профилей 367
7.6. Геометрические характеристики двутавров и швеллеров при свободном и стесненном кручении 368
РАЗДЕЛ 8. ТАБЛИЦЫ ДЛЯ РАСЧЕТА БАЛОК, АРОК И РАМ. Инж. М. С. Волчегорский, инж. Д. Л. Шапиро, д-р техн. наук проф. А. А. Уманский 369
8.1. Балки 369
8.1.1. Эпюры изгибающих моментов и поперечных сил от различных нагрузок 369
8.1.2. Консоль. Опорные реакции, моменты, прогибы и углы поворота концевого сечения 372
8.1.3. Простая балка. Опорные реакции, изгибающие моменты, прогибы, углы поворота опорных сечений, грузовые члены 374
8.1.4. Однопролетные балки с одним защемленным и другим шарнирно опертым концом и с обоими защемленными концами. Опорные реакции и опорные моменты 384
8.1.5. Прогибы однопролетных балок с одним защемленным и другим шарнирно опертым концом и с обоими защемленными концами 389
8.1.6. Прогибы в сечениях с простой балки от сосредоточенного груза Р в сечении х 390
8.1.7. Коэффициенты приведения нагрузки к эквивалентной равномерно распределенной интенсивностью Pэк для определения опорных моментов в неразрезных балках 393
8.1.8. Неразрезные равнопролетные балки. Изгибающие моменты, поперечные силы и опорные реакции от различных нагрузок а) Двух-, трех-, четырех- и пятипролетные балки. б) Бесконечная балка с равными пролетами. в) Определение абсциссы (х0) максимальных пролетных моментов в неразрезных балках 394
8.1.9. Неразрезные равнопролетные балки. Моменты, поперечные силы в сечениях (через 0.1l) и опорные реакции от равномерно распределенной нагрузки: постоянной g и временной р (таблицы Винклера) 401
8.1.10. Неразрезные равнопролетные балки. Моменты, поперечные силы а различных сечениях и опорные реакции от сосредоточенных грузов: постоянных G и временных Р 403
8.1.11. Опорные моменты в неразрезных равнопролетных балках с одним защемленным концом 406
8.1.12. Опорные моменты в неразрезных равнопролетных балках с обоими защемленными концами 406
8.1.13. Прогибы в равнопролетных неразрезных балках (в середине пролета) 408
8.1.14. Опорные моменты в неразрезных равнопролетных балках при осадке опор а) Двух-, трех-, четырех- ч пятипролетные балки. б) Полубесконечная балка. в) Бесконечная балка 410
8.1.15. Ординаты инфлюент (линий влияния) изгибающих моментов и поперечных сил для неразрезных равнопролетных балок 411
8.1.16. Данные для расчета однопролетных подкрановых балок под один кран 413
8.1.17. Данные для расчета неразрезных пятипролетных балок с равными пролетами под два одинаковых крана. Огибающие эпюры М и Q 414
8.1.18. Данные для расчета балок и ригелей рам с вутами а) Симметричная шарнирно опертая по концам балка с вутами. б) Симметричная с защемленными концами балка с вутами. в) Балка с левым односторонним вутом, шарнирно опертая по концам .г) Балка с левым односторонним вутом, защемленная левым концом и шарнирно опертая правым .д) Балка с левым односторонним вутом и обоими защемленными концами. е) Неразрезные равнопролетные балки с симметричными вутами 417
8.1.19. Ординаты инфлюент опорного момента бесконечной балки на упруго оседающих опорах 423
8.1.20. Ординаты инфлюент опорного момента Мг полубесконечной балки на упруго оседающих опорах 423
8.1.21. Данные для расчета перекрытий с перекрестными балками (кессонные перекрытия).а) Схемы распределения нагрузки в перекрестных балках. б) Нагрузки и изгибающие моменты в перекрестных балках при квадратных в плане перекрытиях 424
8.1.22. Усилия в элементах шпренгельной балки. а) Статически определимый шпренгель. б) Статически неопределимый шпренгель 425
8.1.23. Данные для расчета балок с защемленными концами, с ломаной в плане осью 427
8.2. Арки 430
8.2.1. Геометрические данные осей параболической и круговой арок 430
8.2.2. Симметричные трехшарнирные арки любого очертания. Распоры, опорные реакции и изгибающие моменты от различных нагрузок 431
8.2.3. Трехшарнирные круговые и параболические арки. Опорные реакции, изгибающие моменты, поперечные и продольные силы от равномерно распределенной нагрузки 433
8.2.4. Трехшарнирная параболическая арка. Изгибающие моменты в различных сечениях, опорные реакции и распоры от сосредоточенного груза 435
8.2.5. Трехшарнирная параболическая арка. Изгибающие моменты в различных сечениях, опорные реакции и распоры от односторонней частичной равномерно распределенной нагрузки 435
8.2.6. Трехшарнирная параболическая арка. Изгибающие моменты в различных сечениях, опорные реакции и распоры от односторонней частичной равномерно распределенной нагрузки 436
8.2.7. Двухшарнирная параболическая арка. Изгибающие моменты, распоры и опорные реакции от различных нагрузок 437
8.2.8. Двухшарнирная параболическая арка. Изгибающие моменты в различных сечениях, распоры и опорные реакции от действия вертикальной сосредоточенной силы 440
8.2.9. Двухшарнирная параболическая арка. Изгибающие моменты в различных сечениях, опорные реакции от симметричной равномерно распределенной нагрузки 441
8.2.10. Двухшарнирная параболическая арка. Изгибающие моменты в различных сечениях, распоры и опорные реакции от симметричной частичной равномерно распределенной нагрузки 442
8.2.11. Бесшарнирные параболические арки а) Изгибающие моменты, распоры и опорные реакции от различных нагрузок. б) Инфлюенты распора, опорной реакции, опорного момента и момента в середине пролета 443
8 2.12. Дополнительные геометрические данные для параболических, круговых и эллиптических арок 447
8.2.13. Бесшарнирная параболическая арка постоянной толщины. Изгибающие моменты, распоры и опорные реакции от различных нагрузок 447
8.2.14. Поправочные коэффициенты для определения усилий в бесшарнирной параболической арке переменной толщины 449
8.2.15. Опорные моменты от собственного веса бесшарнирных параболических арок переменной толщины 449
8.2.16. Бесшарнирная круговая арка постоянной толщины. Изгибающие моменты, распоры и опорные реакции от различных нагрузок 450
8.2.17. Поправочные коэффициенты для определения усилий в бесшарнирной круговой арке переменной толщины 452
8.2.18. Опорные моменты и распоры от собственного веса бесшарнирных круговых арок переменной толщины 452
8.2.19. Бесшарнирная эллиптическая арка постоянной толщины. Изгибающие моменты, распоры и опорные реакции от различных нагрузок 453
8.2.20. Поправочные коэффициенты для определения усилий в бесшарнирной эллиптической арке переменной толщины 454
8.3. Рамы 455
8.3.1. Моменты в Г-образной раме с горизонтальным или наклонным ригелем. а) Ригель и стойка шарнирно оперты. б) Ригель шарнирно оперт, стойка защемлена 455
8.3.2. Моменты в Г-образной раме с горизонтальным или наклонным защемленным ригелем и защемленной стойкой 457
8.3.3. Моменты в Т-образной раме с шарнирно опертым ригелем и защемленной стойкой 459
8.3.4. Моменты в Т-образной раме с защемленными ригелем и стойкой 461
8.3.5. Моменты и реакции П-образной рамы с шарнирно прикрепленным ригелем. а) Стоики постоянного сечения. б) Стойки ступенчатого сечения 463
8.3.6. Моменты и реакции П-образной рамы. а) С шарнирно прикрепленными стойками. б) С защемленными стойками 465
8.3.7. Моменты в Г-образной раме с горизонтальным или наклонным шарнирно опертым ригелем и ступенчатой защемленной стойкой 467
8.3.8. Моменты в Г-образной раме с горизонтальным или наклонным защемленным ригелем и ступенчатой защемленной стойкой 468
8.3.9. Моменты в Т-образной раме с шарнирно опертым ригелем и ступенчатой защемленной стойкой 470
8.3.10. Моменты в Т-образной раме с защемленным ригелем и ступенчатой защемленной стойкой 472
8.3.11. Простые симметричные рамы. Вспомогательные формулы к 5.6.6 а) Характеристики гибкости рамы, увеличенные в ЕI раз. б) Эпюры M и фиктивные нагрузки ломаного ригеля приведенные к точкам А, С, В. в) Эпюры М и фиктивные нагрузки левой ступенчатой стойки, увеличенные в ЕI раз. Моменты и реакции ступенчатой стойки, защемленной на одном конце и шарнирно опертой на другом конце 474
8.3.12. Моменты и реакции ступенчатой стойки, защемленной на одном конце и шарнирно опертой на другом конце 477
8.3.13. Коэффициенты k0 для определения в ступенчатых стойках: а) перемещения верха защемленной внизу стойки от силы Х=1. б) реакции Нb в случае стойки, защемленной внизу и шарнирно опертой наверху, от взаимного горизонтального смещения опор на =1; в) реакции Нb от поворота нижнего сечения на угол = 1 479
8.3.14. Ступенчатая стойка с защемленным нижним и шарнирно опертым верхним концом. а) Реакции Нb от действия момента Мв = Ра. б) Реакции Hb от действия момента Ми=Ран. в) Реакции Hb от действия горизонтальной силы Р. г) Реакции Нb от действия горизонтальной силы Pн. д) Реакции Нb от действия горизонтальной равномерно распределенной нагрузки рв. е) Реакции Нb от действия горизонтальной равномерно распределенной нагрузки рн. ж) Реакции Нb от действия горизонтальной равномерно распределенной нагрузки по всей высоте стойки. з) Реакции Нb от действия горизонтальной треугольной нагрузки 480
8.3.15 Моменты и реакции ступенчатой стойки с защемленными концами 487
8.3.16. Ступенчатая стойка с защемленными концами. Моменты защемления при различных n и l.а) от поворота верхнего сечения на угол = 1; б) от поворота нижнего сечения на угол =1; в) от взаимного смещения опорных сечений на =1; г) от равномерно распределенной нагрузки; д) от сосредоточенной силы; е) от внешнего момента 488
8.3.17. Расчет одноэтажных многопролетных рам с шарнирно опертыми ригелями и ступенчатыми защемленными стойками. а) Горизонтальная сосредоточенная нагрузка. б) Горизонтальная равномерно распределенная нагрузка. в) Действие внешнего момента на стойку рамы. г) Примеры 491
8.3.18. Изгибающие моменты в одноэтажных многопролетных рамах. а) Двухпролетные рамы. б) Трехпролетные рамы. в) Четырехпролетные рамы. г) Примеры 495
8.3.19. Изгибающие моменты в ригелях многоэтажных рам с равными пролетами 503
8.3.20. Формулы для подсчета интегралов Мора 506
8.4. Балки на упругом (винклеровском) основании 508
8.4.1. Гиперболо-круговые функции для расчета балок на упругом основании и цилиндрических резервуаров 508
8.4.2. Начальные параметры балок на упругом основании 513
8.4.3. Затухающие функции для расчета балок на упругом основании и цилиндрических резервуаров 514
8.4.4. Перемещения и усилия полубесконечной балки от сосредоточенной силы Р= 1 (инфлюенты) 516
8.4.5. Перемещения и усилия полубесконечной балки от сосредоточенного момента L= 1 (инфлюенты) 517
РАЗДЕЛ 9. БРУСЬЯ, ОЧЕРЧЕННЫЕ ПО ДУГЕ КРУГА, И КРУГОВЫЕ КОЛЬЦА. Канд. техн. наук доц. Ю. П. Григорьев 519
9.1. Нагрузка в плоскости кривизны 519
9.1.1. Круговые брусья. Основные обозначения и общие указания. Формулы для усилий и перемещений при простейших нагрузках. Общие формулы для усилий и перемещений. Усилия в ключевом сечении бруса, защемленного двумя концами 519
9.1.2. Круговые кольца. Формулы для усилий и перемещений при простейших нагрузках. Расчет круговых шпангоутов. Формулы для расчета круговых колец, нагруженных произвольным числом сосредоточенных сил и моментов 524
9 2. Нагрузка, перпендикулярная плоскости кривизны 531
9.2.1. Круговые брусья. Основные обозначения и общие указания. Формулы для усилий и перемещений кругового бруса при простейших нагрузках. Общие формулы для расчета 6pуca, нагруженного сосредоточенными силами и моментами. Усилия в ключевом сечении тонкостенного бруса, защемленного двумя концами. Монорельс на трех и на четырех равноотстоящих опорах 531
9.2.2. Расчет массивных и тонкостенных круговых колец при статически определимом опирании 541
9.2.3. Расчет круговых колец на равноотстоящих опорах 546
9.3. Брусья большой кривизны. Напряжение при изгибе. Перемещения при изгибе в плоскости кривизны 551
Раздел 10. ФЕРМЫ. Канд. техн. наук А. Г. Иммерман 553
10.1. Плоские фермы 553
10.1.1. Элементы и классификация плоских ферм 553
10.1.2. Основные положения расчета 553
10.1.3. Определение усилий в статически определимых фермах при неподвижной нагрузке. Установление неработающих стержней и стержней, усилия в которых определяются местной нагрузкой. Аналитическое определение усилий. Графическое определение усилий. Определение усилий по готовым формулам, таблицам и графикам. Расчет ферм на внеузловую нагрузку. Расчет составных ферм. Фермы с гибкими пересекающимися раскосами. Фермы с «окном». Способ замены стержней. Тонкостенные фермы. Распорные и комбинированные фермы 555
10.1.4. Перемещения узлов статически определимых ферм. Исходные данные для определения перемещений. Аналитическое определение перемещений. Графическое определение перемещений. Построение эпюры прогибов пояса фермы по способу фиктивных грузов 560
10.1.5. Инфлюенты усилий и перемещений в статически определимых фермах. Статический способ построения инфлюент усилий. Кинематический способ построения инфлюент усилий. Инфлюента перемещения. Невыгодная установка грузов на инфлюенте 563
10.1.6. Определение усилий в статически неопределимых фермах при неподвижной нагрузке. Приближенные способы расчета. Метод сил. Метод заданных напряжений. Фермы с нецентрированными узлами. Учет жесткости узлов. Учет защемления ферм, жестко связанных с колоннами. Работа нулевых стержней. Проверка расчета ферм 566
10.1.7. Определение перемещений в статически неопределимых фермах 569
10.1.8. Инфлюенты усилий в статически неопределимых фермах 569
10.2. Плоские фермы, соединенные связями (биконструкции) 570
10.2.1. Определение и классификация 570
10.2.2. Основные положения расчета 570
10.2.3. Определение усилий в биконструкциях 571
10.2.4. Статически неопределимые и многорядные биконструкции 572
10.3. Пространственные фермы 573
10.3.1. Классификация и основные положения образования и расчета 573
10.3.2. Общие методы определения усилий 574
10.3.3. Расчет куполов 576
10.3.4. Расчет башен и мачт 576
10.4. Предварительно напряженные фермы 577
10.4.1. Определение. Основные положения расчета и конструирования 577
10.4.2. Фермы с предварительно напряженными отдельными стержнями 577
10.4.3. Предварительно напряженные фермы с затяжками 578
РАЗДЕЛ 11. ТЕОРИЯ УПРУГОСТИ. Д-р техн. наук проф. И. И. Гольденблат 581
11.1. Основные уравнения теории упругости 581
11.1.1. Уравнения равновесия 581
11.1.2. Уравнения совместности деформаций 582
11.1.3. Определение перемещений по заданным составляющим тензора деформаций 583
11.1.4. Схемы решения задач теории упругости. Уравнения Ляме 584
11.1.5. Потенциальная энергия деформации. Начало наименьшей работы 585
11.1.6. Некоторые частные решения 585
11.2. Плоская задача 585
11.2.1. Плоское напряженное состояние 585
11.2.2. Плоская деформация 585
11.2.3. Функция напряжений для плоской задачи 586
11.2.4. Плоская задача в полярных координатах 586
11.2.5. Сведение плоской задачи к задаче об изгибе пластинки 587
11.3. Вариационные методы решения задач теории упругости 588
11.3.1. Метод Ритца 588
11.3.2. Метод Галеркина 590
11.3.3. Метод Треффца (метод смягчения граничных условий) 591
11.4. Метод сеток 591
11.4.1. Тринадцатичленное уравнение 591
11.4.2. Применение метода конечных разностей к расчету балки-стенки 592
11.5. Сводка некоторых решений теории упругости 594
11.5.1. Чистый изгиб 594
11.5.2. Поперечный изгиб консоли 594
11.5.3. Поперечный изгиб балки 595
11.5.4. Изгиб кривого бруса (задача X. С. Головина) 596
11.5.5. Клин, сжатый сосредоточенной силой 596
11.5.6. Толстостенные цилиндры и сферический сосуд 596
11.5.7. Упругая полуплоскость и упругое полупространство 597
11.6. Концентрация напряжений 597
11.6.1. Концентрация напряжений при растяжении 597
11.6.2. Концентрация напряжений при изгибе (инж. Г. Ю. Ратновская). Балка с круглым отверстием. Балка с отверстием квадратной формы 598
11.7. Кручение стержня прямоугольного поперечного сечения 599
11.8. Балки-стенки 600
11.8.1.Однопролетная балка-стенка 600
11.8.2. Многопролетная балка-стенка 600
11.9. Панели крупнопанельных и каркасно-панельных зданий 605
РАЗ

Прочность корпуса водного транспорта

При расчете на местную прочность отдельные конструкции корпуса судна представляются в виде перекрытий, рам, изолированных балок и пластин.

Перекрытие — это система пересекающихся и взаимно связанных балок, концы которых закреплены на так называемом опорном контуре. Опорный контур днищевых и палубных перекрытий образуют борта судна и поперечные переборки, опорный контур бортовых перекрытий — поперечные переборки, днище и палуба судна.

Балки перекрытия располагают параллельно сторонам опорного контура (рис. 1, а). Те балки, которых в перекрытии больше, называются балками главного направления; балки, перпендикулярные им, называются перекрестными балками.

При расчете перекрытия полагают, что нагрузка воспринимается балками главного направления и передается перекрестным балкам, которые должны иметь достаточную жесткость, так как они предназначены для разгрузки балок главного направления. Если жесткость перекрестных балок мала, то они могут даже загружать балки главного направления, что иногда используется для разнесения сосредоточенных нагрузок на большее число балок главного направления.

 

Днищевые перекрытия рассчитывают на действие нагрузки от гидростатического давления забортной воды, веса грузов, оборудования и механизмов, находящихся на днище. Нагрузка должна соответствовать тому положению судна на волне, для которого вычислены напряжения от общего изгиба.

Расчет бортовых перекрытий производят на гидростатическую нагрузку, распределенную по треугольнику и отвечающую положению судна на волне. Местная прочность связей палубного перекрытия проверяется на действие равномерно распределенной нагрузки от веса находящегося на палубе груза и веса воды, попадающей на палубу во время шторма. Нагрузки, на которые рассчитываются перекрытия, регламентируются «Нормами прочности морских судов».

Если число балок обоих направлений небольшое, то перекрытия рассчитывают методом приравнивания прогибов. При нескольких перекрестных балках расчет перекрытия может быть сведен к расчету балок главного направления, загруженных реакциями со стороны перекрестных связей и внешней нагрузкой (рис.1, а). Если число балок главного направления велико, то они как бы создают для перекрестных балок упругое основание. В этом случае расчет перекрытия сводится к расчету перекрестных балок на упругом основании.

 

Конструктивные элементы и связи корпуса судна:

а — ахтерпиковая переборка, b — коробчатая балка, с — надстройка, d — носовая оконечность, е — кормовая оконечность, f — район грузового люка, g — район между грузовыми люками, h — район машинного отделения, i — главная палуба в районе угла грузового люка 1 — палуба ахтерпиковой цистерны; 2 — дейдвудная труба; 3 — верхний пояс обшивки; 4 — стенка; 5 — нижний пояс обшивки; 6 — настил палубы; 7 — продольный комингс люка; 8 — поперечный комингс люка; 9 — ширстрек; 11 — скуловой пояс; 12 — настил второго дна; 13 — днищевая обшивка; 14 — цепной ящик; 15 — твиндек; 16 — таранная переборка; 17 — ют; 18 — аварийный выход; 19 — ахтерпик; 20 — гребной вал; 21 — дейдвудная труба; 22 — ахтерштевень; 23 — перо руля; 24 — баллер руля; 25 — бак; 26 — форпик; 27 — бортовой стрингер; 28 — твиндечный шпангоут; 29 — трюмный шпангоут; 30 — верх-ная (главная) палуба; 31 — туннель гребного вала; 32 — карлингсы; 33 — днищевые стрингеры; 34 — вертикальный киль; 35 — машинная шахта; 36 — верхний световой люк; 37 — навигационный мостик; 38 — шлюпочная палуба; 39 — палуба средней надстройки; 40 — верхняя (главная) палуба; 41 — фундамент главного двигателя; 42 — шпангоут надстройки; 43 — крайний междудонный лист; 44 — рамный бимс; 45 — рамный шпангоут; 46 — ромбоидальный лист-накладка; 47 — пиллерс; 48 — носовые брештуки; 49 — продольное ребро.

 

Под рамами понимают балки набора, расположенные в одной плоскости и жестко соединенные между собой. На рис. 1, б показаны схемы шпангоутных рам однопалубного и двухпалубного судна. Рамы состоят из флора, шпангоутов и бимсов. Поскольку у промысловых судов флоры значительно больше шпангоутов, полагают, что шпангоуты жестко заделаны на флорах, и производят расчет шпангоутных рам без днищевых ветвей (рис. 1, б). Шпангоутные рамы однопалубных судов рассчитывают методом трех моментов, многопалубных судов — методом угловых деформаций. Расчетной является гидростатическая нагрузка, распределенная по всей высоте борта по закону треугольника.

 

Изолированные балки — это такие балки, прочность которых может быть рассчитана отдельно от прочности перекрытия. Они намного меньше других связей перекрытия. К числу изолированных балок относятся, например, ребра жесткости, установленные по днищу между флорами. Вследствие симметрии конструкции и нагрузки такие ребра жесткости рассчитывают как балки, жестко заделанные на флорах и загруженные давлением воды (рис. 1, в).

Под пластинами понимают части листов наружной обшивки, настилов палуб, платформ и двойного дна между балками набора (рис. 1, г). Балки набора служат для пластины опорным контуром. Как правило, пластины имеют симметричные пролеты и нагрузку, поэтому их можно считать жестко заделанными на опорном контуре. Если отношение сторон опорного контура велико, то пластину можно полагать гнущейся в средней части по цилиндрической поверхности. В этом случае расчет пластины сводится к расчету балки единичной ширины, вырезанной из пластины вдоль короткой стороны.

Поскольку пластины участвуют в изгибе вместе с балками набора, в расчетное сечение балок включают части пластин, прилегающие к балкам—так называемые присоединенные пояски. Ширина присоединенного пояска определяется по «Нормам прочности».

В связях, участвующих одновременно в обеспечении общей и местной прочности, производится суммирование напряжений от общего и местного изгибов. Например, в днищевой обшивке суммируются напряжения от общего изгиба, изгиба днищевой пластины вместе с продольными балками набора и изгиба самой пластины. Напряжения от местного изгиба позволяют оценить местную прочность судовых конструкций, а суммарные напряжения от общего и местного изгибов — общую прочность корпуса судна.

Экспериментальные исследования систем перекрестных балок из деревянных элементов на квадратном плане при изменении динамических и статических нагрузок Текст научной статьи по специальности «Строительство и архитектура»

УДК 624.072.2.011.1

DOI: 10.17238/issn0536-1036.2017.5.119

ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ

СИСТЕМ ПЕРЕКРЕСТНЫХ БАЛОК ИЗ ДЕРЕВЯННЫХ ЭЛЕМЕНТОВ НА КВАДРАТНОМ ПЛАНЕ ПРИ ИЗМЕНЕНИИ ДИНАМИЧЕСКИХ И СТАТИЧЕСКИХ НАГРУЗОК

A.В. Турков, д-р техн. наук, зав. каф.

B.И. Коробко, д-р техн. наук, проф. каф. А.А. Макаров, аспирант

Приокский государственный университет, Наугорское шоссе, д. 29, г. Орел, Россия, 302020; е-mail: [email protected], [email protected], [email protected]

Рассмотрены результаты экспериментального изучения системы перекрестных балок из деревянных элементов на квадратном плане при изменении жесткости узловых соединений. Определена фактическая податливость узловых соединений по результатам экспериментально-теоретических исследований. В ходе эксперимента проведены статистические и динамические испытания, в результате которых получены максимальный прогиб и частота собственных колебаний системы. Установлено, что при уменьшении жесткости узлового соединения максимальный прогиб увеличивается, частота собственных колебаний системы снижается. Сопоставлены теоретические и экспериментальные данные: экспериментальные прогибы и частоты больше полученных расчетным путем. Разница между экспериментальными и теоретическими прогибами достигает 7,54 %, по частотам собственных колебаний — 0,69 %. Основанием для подобных расхождений являлось то обстоятельство, что за счет высокой степени податливости узлов системы ее деформирование при высоких уровнях нагрузки происходит в нелинейной области. Разница между теоретическими и экспериментальными значениями коэффициента, связывающего частоту основного тона собственных поперечных колебаний, распределенную по площади массу конструкции и максимальный прогиб при действии равномерно распределенной нагрузки, достигает 7,97 %. На основании исследования можно сделать вывод о достаточно хорошей сходимости значений численных и экспериментальных прогибов и частот собственных колебаний, а также о применимости этого экспериментального коэффициента для систем перекрестных балок.

Ключевые слова: система перекрестных балок, испытательный стенд, динамические испытания, статические испытания, модуль упругости, частота собственных колебаний, максимальный прогиб.

Для цитирования: Турков А.В., Коробко В.И., Макаров А.А. Экспериментальные исследования систем перекрестных балок из деревянных элементов на квадратном плане при изменении динамических и статических нагрузок // Лесн. журн. 2017. № 5. С. 119-126. (Изв. высш. учеб. заведений). DOI: 10.17238/issn0536-1036.2017.5.119

Введение

Системы перекрестных балок (СПБ) являются одними из самых эффективных деревянных пространственных конструкций. Исследованиями СПБ занимались такие крупные ученые, как Э.Н. Байда [1], В.А. Игнатьев [2], Б.Н. Кутуков [7], Е.И. Светозарова и Б.В. Лабудин [8-12], Л.Н Лубо [13], A. Yettram и H. Husrnn [18], W. Martin [16], P. Ма8е [17] и др. Вопросам взаимосвязи максимальных прогибов и частот собственных колебаний балок и пластинок посвящены работы В.И. Коробко, А.В. Туркова и К.В. Марфина [3-6, 15], для СПБ выполнены исследования А.В. Туркова и А.А. Макарова [14].

Цель данного исследования — получение экспериментальных статических и динамических параметров СПБ и сопоставление их с численными данными для оценки применимости формулы В.100 мм длиной 590 мм, которые в узлах соединяются с помощью стальных гнутых уголков из листа толщиной 1 мм на болтах М6. Размер СПБ в плане — 2400×2400 мм, размер ячейки — 600×600 мм.

Вначале экспериментально определяли фактическую податливость узловых соединений. Элементы СПБ моделировали стержнями со вставками на концах [15], которые в свою очередь характеризовали податливость узловых соединений. По результатам расчетов и экспериментальным прогибам и частотам колебаний определяли фактическую податливость узлов при креплении элементов нагелями (болтами), для 4 болтов — Е1вс/Е1эл = 0,0033, для 2 болтов — Е/вс/Е/эл = 0,0013 (здесь Е1вс и Е1эл — соответственно изгибная жесткость вставки и деревянного элемента СПБ).

Для определения прогиба СПБ нагружали статической сосредоточенной нагрузкой во всех узлах (кроме опорных) пятью (1-5) ступенями. Вес каждой ступени в пересчете на равномерно распределенную нагрузку 15,625 Н/м2. После снятия показаний (по индикатору) от максимальной нагрузки, которая составляла 78,125 Н/м , СПБ разгружали и после 15 мин «отдыха» снова загружали. Для каждого типа СПБ испытания проводили не менее 3 раз до получения стабильных значений экспериментальных прогибов (в табл. 1).

Таблица 1

Экспериментальный максимальный прогиб (мм) СПБ при различной податливости узловых соединений

Ступень Нагрузка, Н/м2 Максимальный прогиб при количестве болтов в узле, шт.

4 2

1 15,625 0,35 3,88

2 31,25 2,77 7,58

3 46,875 4,18 10,21

4 62,50 5,80 14,37

5 78,125 7,49 18,90

После каждого этапа статических испытаний опытную конструкцию разгружали и давали ей «отдыхать» в течение 15…20 мин, после чего проводили динамические испытания, в ходе которых определяли основные круговые частоты собственных поперечных колебаний СПБ в зависимости от податливости узловых соединений. Измерение основных частот колебаний выполняли на виброанализаторе «ВИБРАН-2.0». Датчик закрепляли снизу, в центральном узле СПБ, колебания возбуждали путем удара сверху резиновой киянкой по центральному узлу конструкции. Для каждого типа СПБ динамические испытания проводили не менее 3 раз до стабильных значений экспериментальных круговых частот колебаний.

Характерные виброграммы, полученные в ходе эксперимента, представлены на рис. 2, результаты измерения частот колебаний — в табл. 2.

4 5

а б

Рис. 2. Характерные виброграммы собственных колебаний СПБ: а — 4 болта в узле;

б — 2 болта в узле

Таблица 2

Экспериментальная частота собственных колебаний (с ) СПБ при различной жесткости крепления узловых соединений

Значение показателя при количестве болтов в узле, шт.

4 2

Частота / 14,00 9,00

Круговая частота, ю 87,92 56,52

Результаты исследования и их обсуждение

При сопоставлении результатов экспериментальных и численных исследований критерием точности является коэффициент К, связывающий частоту ю основного тона собственных поперечных колебаний СПБ, распределенную по площади массу конструкции т и максимальный прогиб Ж0 при действии равномерно распределенной нагрузки q в формуле В.И. Коробко [3]:

Ж0 ю2 = К1.

т

Для квадратных пластин с шарнирно опертым контуром К = 1,582.

Анализ полученных данных показал, что экспериментальные прогибы и частоты собственных колебаний больше численных (аналитических). Для СПБ при креплении узла на 4 болтах разница между экспериментальными и численными значениями прогибов составляла 1,87 %, на 2 болтах — 7,54 %, между частотами -соответственно 0,09 и 0,69 %. Для коэффициента К расхождение между аналитическими и экспериментальными данными — соответственно 1,98 и 7,97 %.

Основной причиной расхождения экспериментальных и численных значений прогибов и частот поперечных колебаний являлось то обстоятельство, что за счет высокой степени податливости узлов деформации СПБ при высоких уровнях нагрузки происходили в нелинейной области.

Заключение

На основании проведенного исследования можно сделать вывод о достаточно хорошей сходимости значений численных и экспериментальных прогибов и частот собственных колебаний, а также о соответствии экспериментального коэффициента К его аналитическим значениям.

СПИСОК ЛИТЕРАТУРЫ

1. Байда Э.Н., Лабудин Б.В. Об одном методе расчета регулярных ортогональных перекрестных систем // Конструкции из клееной древесины и пластмасс. Л.: ЛИСИ, 1978. С. 36-40.

2. Игнатьев В.А. Расчет регулярных стержневых систем. Саратов: Сарат. ун-т, 1973. 433 с.

3. Коробко В.И. Об одной «замечательной» закономерности в теории упругих пластинок // Строительство и архитектура. 1989. № 11. С. 32-36. (Изв. высш. учеб. заведений).

4. Коробко В.И., Турков А.В. Поперечные колебания и прогибы однопролетных балок, подкрепленных в пролете упругими опорами // Строительная механика инженерных конструкций и сооружений. 2007. № 1. С. 53-55.

5. Коробко В.И., Турков А.В. Способ определения жесткости вертикального стыка составной балки // Лесн. журн. 2010. № 1. С. 88-92. (Изв. высш. учеб. заведений).

6. Коробко В.И., Турков А.В., Бояркина О.В. Закономерности поперечного изгиба и свободных колебаний упругих балок и пластинок // Строительная механика и расчет сооружений. 2006. № 4. С. 64-69.

7. Кутуков В.Н. Некоторые задачи статического и динамического расчета регулярных систем // Расчет пространственных конструкций. Вып. 4. М.: Стройиздат, 1958. С. 225-238.

8. Лабудин Б.В. Влияние некоторых факторов на материалоемкость перекрестно-балочных конструкций из клееных деревянных элементов // Исследование конструкций из клееной древесины и пластмасс. 1977. № 1. С. 89-93.

9. Лабудин Б.В. К вопросу о расчете перекрестных балок из сборных клееных деревянных элементов с учетом податливости узлов // Конструкции из клееной древесины и пластмасс: межвуз. сб. Л.: ЛИСИ, 1979. С. 65-71.

10. Лабудин Б.В. Расчет перекрестных систем с использованием матрицы жесткости коробчатого элемента на упруго-податливых связях // Конструкции из клееной древесины и пластмасс: межвуз. сб. Л.: ЛИСИ, 1980. С. 8-11.

11. Лабудин Б.В. Расчет плитно-ребристых конструкций с упруго-податливыми связями // Лесн. журн. 1992. № 1. С. 67-72. (Изв. высш. учеб. заведений).

12. Лабудин Б.В., Светозарова Е.И. Пространственные перекрестно-балочные покрытия из клееных деревянных элементов // Исследование конструкций из клееной древесины и пластмасс. 1977. № 1. С. 41-47.

13. Лубо Л.Н., Миронков Б.А. Плиты регулярной пространственной структуры. Л.: Стройиздат, 1976. 126 с.

14. Турков А.В., Макаров А.А. Прогибы и частоты собственных колебаний систем перекрестных балок на квадратном плане с учетом податливости узловых соединений // Строительство и реконструкция. 2013. № 1. С. 33-36.

15. Турков А.В., Марфин К.В. Исследование прогибов и частот собственных колебаний составных круглых транстропных пластин // Лесн. журн. 2013. № 4. С. 66-71. (Изв. высш. учеб. заведений).

16. Martin W. Berechnung einer Fachwerkplatte // Wissenschaftliche Zeitschrift der Hochschule fur Bauwesen Leipzig. 1966. Heft 4.

17. Mase P. Analysis of Building Grid Floare // Journal of the Institution of Engineers (India): Civil Engineering Division. 1960. Vol. 41, no. 7. Part 4.

18. Yettram A.L., Husain H.M. The Representation of a Plate in Flexure by a Grid of Orthogonally Connected Beams // International Journal of Mechanical Sciences. 1965. Vol. 7, iss. 4. Pp. 243-251.

Поступила 24.02.17

UDC 624.072.2.011.1

DOI: 10.17238/issn0536-1036.2017.5.119

The Experimental Studies of Cross-Beam Systems of Wood Members on a Square Plan when Dynamic and Static Load Variation

A. V. Turkov, Doctor of Engineering Sciences, Head of Department V.I. Korobko, Doctor of Engineering Sciences, Professor A.A. Makarov, Postgraduate Student

Prioksky State University, Naugorskoe sh., 29, Orel, 302020, Russian Federation; e-mail: [email protected], [email protected], [email protected]

The paper presents the results of experimental studies of the cross-beam system of wood members on a square plan with a change in the rigidity of node connections. We determine the actual compliance of node connections by the results of the experimental and theoretical studies. In the experiment, statistic and dynamic tests are performed, and the maximum deflection and free frequency of the system are obtained. The maximum deflection increases, free frequency of the system decreases when the stiffness of the node connection decreases. We compare the theoretical and experimental data: the experimental deflections and frequencies are greater than the parameters, obtained by means of a calculation. The difference between the experimental and theoretical deflections is 7.54 %, and 0.69 % is in terms of free frequency. The reason for such discrepancies is the fact that the system deformation at high load levels occurs in the nonlinear region due to the high degree of compliance of the system nodes. The difference between theoretical and experimental data reaches 7.97 % for the coefficient connecting base frequency of free transverse vibrations, mass of the structure distributed over the area and the maximum deflection under the action of an evenly distributed load. Based on the study, wet can conclude about fine precision of numerical and experimental deflections and free frequencies, and about the applicability of this experimental coefficient for cross-beam systems.

Keywords: cross-beam system, testing stand, dynamic test, static test, elasticity modulus, free frequency, maximum deflection.

For citation: Turkov A.V., Korobko V.I., Makarov A.A. The Experimental Studies of Cross-Beam Systems of Wood Members on a Square Plan when Dynamic and Static Load Variation. Lesnoy zhurnal [Forestry journal], 2017, no. 5, pp. 119-126. DOI: 10.17238/ issn0536-1036.2017.5.119

REFERENCES

1. Bayda E.N., Labudin B.V. Ob odnom metode rascheta regulyarnykh ortogonal’nykh perekrestnykh sistem [On a Method for Calculating Regular Orthogonal Cross Systems]. Konstruktsii iz kleenoy drevesiny i plastmass [Structures of Glued Wood and Plastics]. Leningrad, Leningrad Engineering and Construction Institute Publ., 1978, pp. 36-40. (In Russ.)

2. Ignat’ev V.A. Raschet regulyarnykh sterzhnevykh system [Calculation of Regular Frame Structures]. Saratov, Saratov Higher Military School Publ., 1973. 433 p. (In Russ.)

3. Korobko V.I. Ob odnoy «zamechatel’noy» zakonomernosti v teorii uprugikh plastinok [On a «Remarkable» Regularity in the Theory of Elastic Plates]. Stroitel’stvo i arkhitektura, 1989, no. 11, pp. 32-36.

4. Korobko V.I., Turkov A.V. Poperechnye kolebaniya i progiby odnoproletnykh balok, podkreplennykh v prolete uprugimi oporami [Transverse Oscillations and Deflections of Single Beams Reinforced by Elastic Supports in the Span]. Stroitel’naya mekhanika inzhenernykh konstruktsiy i sooruzheniy [Structural Mechanics of Engineering Constructions and Buildings], 2007, no. 1, pp. 53-55.

5. Korobko V.I., Turkov A.V. Sposob opredeleniya zhestkosti vertikal’nogo styka sostavnoy balki [Method for Determining Vertical Joint Stiffness of Composite Beam]. Lesnoy zhurnal [Forestry journal], 2010, no. 1, pp. 88-92.

6. Korobko V.I., Turkov A.V., Boyarkina O.V. Zakonomernosti poperechnogo izgiba i svobodnykh kolebaniy uprugikh balok i plastinok [Regularities of Transverse Bending and Free Oscillations of Elastic Beams and Plates]. Stroitel’naya mekhanika inzhenernykh konstruktsiy i sooruzheniy [Structural Mechanics of Engineering Constructions and Buildings], 2006, no. 4, pp. 64-69.

7. Kutukov V.N. Nekotorye zadachi staticheskogo i dinamicheskogo rascheta regulyarnykh sistem [Some Problems of Static and Dynamic Calculation of Regular Systems]. Raschet prostranstvennykh konstruktsiy. Vyp. 4 [Space Structures Analysis. Iss. 4]. Moscow, Stroyizdat Publ., 1958, pp. 225-238. (In Russ.)

8. Labudin B.V. Vliyanie nekotorykh faktorov na materialoemkost’ perekrestno-balochnykh konstruktsiy iz kleenykh derevyannykh elementov [Influence of Some Factors on the Material Intensity of Two-Way Beam Structures Made of Glued Wood]. Issledovanie konstruktsiy iz kleenoy drevesiny i plastmass [Investigation of Structures Made of Glued Wood and Plastics], 1977, no. 1, pp. 89-93.

9. Labudin B.V. K voprosu o raschete perekrestnykh balok iz sbornykh kleenykh derevyannykh elementov s uchetom podatlivosti uzlov [On the Calculation of Two-Way Beams from Precast Glued Wood Units, Taking into Account the Joint Mobility]. Konstruktsii iz kleenoy drevesiny i plastmass [Structures of Glued Wood and Plastics]. Leningrad, Leningrad Engineering and Construction Institute Publ., 1979, pp. 65-71. (In Russ.)

10. Labudin B.V. Raschet perekrestnykh sistem s ispol’zovaniem matritsy zhestkosti korobchatogo elementa na uprugo-podatlivykh svyazyakh [Calculation of Cross Systems Using the Stiffness Matrix of a Box-Shaped Element on Elastic-Compliant Constraints]. Konstruktsii iz kleenoy drevesiny iplastmass [Structures of Glued Wood and Plastics]. Leningrad, Leningrad Engineering and Construction Institute Publ., 1980, pp. 8-11. (In Russ.)

11. Labudin B.V. Raschet plitno-rebristykh konstruktsiy s uprugo-podatlivymi svyazyami [Calculation of Slab and Ribbed Structures with Elastic-Compliant Constraints]. Lesnoy zhurnal [Forestry journal], 1992, no. 1, pp. 67-72.

12. Labudin B.V., Svetozarova E.I. Prostranstvennye perekrestno-balochnye pokrytiya iz kleenykh derevyannykh elementov [Spatial Two-Way Beam Roofs Made of Glued Wood]. Issledovanie konstruktsiy iz kleenoy drevesiny i plastmass [Investigation of Structures Made of Glued Wood and Plastics], 1977, no. 1, pp. 41-47.

13. Lubo L.N., Mironkov B.A. Plity regulyarnoy prostranstvennoy struktury [Plates of Regular Spatial Structure]. Leningrad, Stroyizdat Publ., 1976. 126 p. (In Russ.)

14. Turkov A.V., Makarov A.A. Progiby i chastoty sobstvennykh kolebaniy sistem perekrestnykh balok na kvadratnom plane s uchetom podatlivosti uzlovykh soedineniy [Deflections and Frequencies of Own Fluctuations of Systems Cross Beams on the Square Plan Taking into Account Pliability of Nodal Connections]. Stroitel’stvo i rekonstruktsiya [Building and Reconstruction], 2013, no. 1, pp. 33-36.

15. Turkov A.V., Marfin K.V. Issledovanie progibov i chastot sobstvennykh kolebaniy sostavnykh kruglykh transtropnykh plastin [Study of Deflection and Natural Vibration Frequencues of Composite Circular Transtropic Plates]. Lesnoy zhurnal [Forestry journal], 2013, no. 4, pp. 66-71.

16. Martin W. Berechnung einer Fachwerkplatte. Wissenschaftliche Zeitschrift der Hochschule fur Bauwesen Leipzig, 1966, Heft 4.

17. Mase P. Analysis of Building Grid Floare. Journal of the Institution of Engineers (India): Civil Engineering Division, 1960, vol. 41, no. 7, part 4.

18. Yettram A.L., Husain H.M. The Representation of a Plate in Flexure by a Grid of Orthogonally Connected Beams. International Journal of Mechanical Sciences, 1965, vol. 7, iss. 4, pp. 243-251.

Received on February 24, 2017

Перекрестные балочные системы из цельной или клееной древесины

Перекрестные балочные системы образуются балками двух или трех направлений и совместно работающих с ними настилов из досок или плитных материалов. Такие конструкции применяют для перекрытия квадратных или прямоугольных в плане зданий с соотношением сторон не более 1:1,5. При опирании по всему контуру балки одного направления, как правило, вдоль меньшего пролета представляют собой неразрезные конструкции высотой 1/18…1/20 пролета, а балки другого направления образуются вставками между первыми. Вставки соединяются между собой при помощи накладок или металлических стержней, вклеенных в древесину. Могут быть приняты и другие способы образования перекрестных балочных систем.

При опирании системы только в углах или на опоры, шаг которых превышает шаг балок в балочной клетке, предусматриваются обрамляющие балки. Высоту сечения этих балок принимают равной 1/20…1/20 пролета. Размеры ячеек, образуемых балками, назначают 0,75…3 м. Для обеспечения жесткости настилов в ячейках могут располагаться вспомогательные ребра.

Балки, образующие систему, могут выполняться в виде дощатоклееных или двухпоясных клеефанерных элементов. Применяют клеефанерные балки коробчатого и двутаврового сечений с плоской, волнистой или прерывистой стенкой, применение клеефанерных элементов обеспечивает минимальную материалоемкость конструкций.

Перекрестные балочные системы могут применяться как для покрытий, так и для перекрытий.

Расчет перекрестных балочных систем. Статический расчет перекрестных систем проводят методом сил с учетом настила как верхних полок пересекающихся балок или заменяют решетчатую систему сплошной, т. е. рассчитывают как плиту.

При расчете методом сил в качестве основной системы принимают однопролетные балки, в качестве неизвестных — опорные реакции в местах пересечения с балками перпендикулярного направления. Число неизвестных зависит от количества ячеек и от характера приложения нагрузки. При равномерном распределении ее по всей системе с количеством ячеек nxn число неизвестных составляет S = 1/8 (n-1)(n-n) при нечетном п и S=1/8(n-2)n — при четном значении п.

Для решения можно использовать ЭВМ или пользоваться таблицами (табл. 2.13.2). Табл. 2.13.2 составлена для квадратных в плане систем из балок равной жесткости при шарнирном опирании их по контуру. Ячейки — квадратные, количество их — от 4×4 до 6×6, нагрузка — равномерно распределенная.

Для вычисления расчетных значений указанные в табл. 2.13.2 величины необходимо умножить на коэффициенты:

где P — интенсивность равномерно распределенной нагрузки; а — размер ячейки; n — количество ячеек в системе; EI — изгибная жесткость балок системы, 10 кН*м2.

При статическом расчете перекрестных систем с любым прямоугольным планом и любым соотношением размеров ячеек используются таблицы, данные которых получены решением с заменой перекрестной системы сплошной плитой.

При статическом расчете опертых по контуру клеефанерных плит величины расчетных усилий и прогибы можно с достаточной точностью найти, рассматривая конструкцию как перекрестную систему балок. Сечение их, как было указано выше, составляют ребра и фанерные полки шириной аx в одном направлении, фанерные полки шириной аy и арматурные стержни — в другом, а значения моментов инерции сечений, приведенные к фанере, составят: для балок вдоль цельных ребер

для балок вдоль составных ребер

где bp1, bp2 — толщины соответственно сжатой и растянутой фанерных обшивок; h2, h3 — расстояние от нейтральной оси до соответственно сжатой или растянутой кромок, см; аx, аy — расстояние между осями ребер соответствующих направлений; Irx — момент инерции деревянного ребра относительно нейтральной оси сечений, см4; Ea, Ew — модули упругости арматуры и древесины; Ep, Ep90 — модули упругости фанеры вдоль и поперек волокон наружных слоев; Fa1, Fa2 — площадь арматуры сжатой и растянутой зон, см2; ha1, ha2 — расстояние от нейтральной оси до центра тяжести соответственно сжатой и растянутой арматуры, см.

Найдя расчетные усилия по табл. 2.13.2, определяют средние значения нормальных напряжений в фанерных сжатых или растянутых обшивках двух направлений по формуле

Расчёт железобетонных балок прямоугольного сечения при совместном воздействии поперечных сил, крутящих и изгибающих моментов

Аннотация В статье даётся обоснование расчёта железобетонных балок прямоугольного сечения при совместном воздействии поперечных сил, крутящих и изгибающих моментов. Решая проблему обеспечения надёжности и качества объектов строительства в Республике Беларусь, ближнем и дальнем зарубежье, авторы подчёркивают неизбежность расчёта железобетонных конструкций, подверженных кручению с изгибом. Отмечается необходимость проведения экспериментальных и теоретических исследований прочности железобетонных балок криволинейного очертания в плане, бортовых балок железобетонных фундаментов из перекрёстных лент, балок открытых крановых эстакад и путепроводов, балок в пространственных рамных конструкциях и прогонах монолитно связанных с второстепенными опорными конструкциями, так как несущая способность таких элементов при кручении сравнительно ниже, чем при изгибе. Используя тензор напряжений для изгиба, поперечной силы, крутящего момента и совместного воздействия этих факторов, представлено общее положение исследования работы пространственных сечений железобетонных балок прямоугольного сечения, включающее анализ их напряжённого состояния для трёх основных характерных случаев. При расчёте прочности пространственных сечений принята идеализированная двухлинейная диаграмма деформирования согласно ТКП EN 1992-1-1, на основе которой приводится методика расчёта несущей способности железобетонной балки прямоугольного сечения, воспринимающей одновременно крутящий и изгибающий момент. Несущая способность железобетонной балки при совместном воздействии крутящего момента и поперечной силы диктуется условием прочности из соотношения моментов внешних и внутренних сил относительно оси, проходящей через центр тяжести сжатой зоны балки при эпюре напряжений сжатой зоны в виде прямоугольной трапеции. Предложен упрощённый способ расчёта пространственных сечений железобетонных балок прямоугольного сечения.

Ключевые слова: напряжённое состояние, тензор напряжений, поперечное сечение, крутящий момент, изгибающий момент, пространственное сечение, ветви хомутов, ядро сечения

Для цитирования: Семенюк, С.Д. Расчёт железобетонных балок прямоугольного сечения при совместном воздействии поперечных сил, крутящих и изгибающих моментов / С.Д. Семенюк, А.В. Зезюлин, Е.Я. Семенюк // Проблемы современного бетона и железобетона : сб. науч. тр. / Ин-т БелНИИС; редкол.: О. Н. Лешкевич [и др.]. – Минск, 2015. – Вып. 7. – С. 133-151.

Полный текст статьи на русский язык

Список использованных источников

1. Коуэн, Г. Дж. Кручение в обычном и предварительно напряжённом железобетоне / Г. Дж. Коуэн. – М. : Стройиздат, 1972. – 104 с.
2. Савицкий, Н. В. Оценка надёжности железобетонных элементов по прочности сечений наклонных продольной оси /Н. В. Савицкий, К. В. Баташева, А. А. Тытюк, Т. Ю. Шевченко // Сб. наук. тр. ПГАСА. – Донецк: ПГАСА, 2004. – Вып. 29. – С. 98 – 101.
3. Семенюк, С. Д. Влияние предыстории загружения на несущую способность железобетонных балок, подверженных кручению с изгибом / С. Д. Семенюк, И. С. Фролков // Ресурсоекономнi матерiали, конструкциi, будiвлi та споруди : збiрник наукових працъ. – Вып. 22. – Рiвне, 2011. – С. 722 – 727.
4. Семенюк, С. Д. Железобетонные и пространственные фундаменты жилых и гражданских зданий на неравномерно деформированном основании / С. Д. Семенюк. – Могилёв : Белорусско–Российский университет, 2003. – 269 с.
5. Семенюк, С. Д. Расчёт несущей способности железобетонных конструкций, работающих на изгиб с кручением / С. Д. Семенюк, Ю. Г. Москалькова, С. В. Босаков // Ресурсоекономнi матерiали, конструкциi, будiвлi та споруди: збiрник наукових працъ / НУВХП. – Вып. 30. – Рiвне, 2015. – С. 263 – 270.
6. Тимошенко, С. П. Теория упругости / С.П. Тимошенко, Дж. Гудьер. – М. : Наука, 1979. – 560 с.
7. Торяник, М. С. Расчёт железобетонных конструкций при сложных деформациях / М. С. Торяник. – М. : Стройиздат,1974. – 297 с.
8. Фалеев, Л. В. Экспериментально–теоритические исследования несущей способности железобетонных балок прямоугольного и таврового сечений, работающих на косой изгиб с кручением.: Дис. канд. техн. наук / Л. В. Фалеев. – Мн., 1968. – 316 с.
9. Феодосьев, В. И. Сопротивление материалов / В. И. Феодосьев. – М. : Наука, 1979. – 540 с.
10. Юдин, В. К. Работа железобетонных балок прямоугольного сечения на кручение с изгибом / В. К. Юдин // Бетон и железобетон. – 1964. – № 1. – С. 11 – 14.

ISSN 2076-6033

Лучшее руководство по определению прогиба в балках переменного сечения — опытный инженер

Таблицы балок дают информацию и предполагают, что прогиб расчет основан на постоянном сечении. Итак, что нам делать, если у нашей балки есть крест сечение, которое меняется по длине балки?

Чтобы определить величину отклонения в балка переменного сечения, необходимо интегрировать формулу прогиба балки с моментом инерции, являющимся переменной по отношению к длине и применить граничные условия.Луч Формула отклонения: v ’’ = M (x) / [E * I (x)].

Непрерывная или дискретная — Есть два типа секций балки: непрерывная и дискретная. Большинство балок представляют собой непрерывных балок и имеют либо постоянное сечение, либо сечение, которое постепенно изменяется по длине балки. Кровельные балки в больших стальных зданиях — отличный пример непрерывной переменной балки. Балка относительно короткая на концах и очень высокая посередине.

Дискретные балки балки которые имеют внезапные разрывы в разрезе.Вы не поверите, но иногда это проще для расчета, потому что дискретные участки обычно постоянны, что приводит к более легкий расчет.

Формула отклонения балки — универсальная формула, которая позволяет настраивать несколько нагрузок и балку разделы. Предупреждаю, что чем больше чем точнее должен быть ваш расчет, тем сложнее будет выполнить математику. Упрощение здесь сэкономит много времени и усилия. Как упоминалось ранее, формула:

в ’’ = M (x) / [E * I (x)]

Где v ’’ — вторая производная отклонения ( ускорение прогиба), M — момент, который обычно является функцией положение по длине балки, x. E — модуль упругости, I — момент инерции поверхности луч. Все табличные балки будут считайте это постоянной величиной и, следовательно, ни одна из формул прогиба может быть использован.

Теперь, когда мы проинтегрируем приведенное выше уравнение, мы будем выполнение неопределенного интеграла, что означает, что мы должны добавить константу, C _n, к полиному каждый раз, когда мы интегрируем. Поскольку мы будем интегрировать уравнение два раза, мы получим две константы. Если у нас есть дискретный В этом случае у нас будет два или более уравнений.

Граничные условия — это требования, которым должна соответствовать формула прогиба балки, когда она находится в окончательном виде. Окончательная форма приходит только тогда, когда мы используем граничные условия для решения констант образованный неопределенным интегралом. 4.

Теперь мы определим момент и дважды проинтегрируем уравнение прогиба балки, каждый раз добавляя переменную для неопределенного интеграла. Я решил, что моя система координат (переменная x) начинается с основания. Это немного усложняет интегрирование, но переменные C ₁ и C ₂ будут уравновешиваться из-за граничных условий 1 и 2. Вы увидите через секунду.

Мне нужно выполнить интегрирование только для одного из разделов, а затем изменить I ₁ на I ₂ в уравнениях.Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные.

Теперь, когда проблема определена, давайте установим граничные условия. Нам нужно, чтобы положение и наклон на фиксированном конце балки составляли 0 дюймов и 0 радиан. Также нам понадобятся еще два граничных условия на стыке сегментов. Наклон и положение в этом положении должны быть одинаковыми.

Решим граничные условия 1 и 2

Как упоминалось выше, я предвидел, что переменные C1 и C2 будет равно 0, когда я выберу, чтобы система координат начиналась с база.

Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее.

Обратите внимание на проверку, которую я вставил в блок поиска, чтобы чтобы мы могли проверить, что v ₁ = v ₂ и s ₁ = с ₂ при 50 дюйм.Это подтверждает что положение и наклон в этой точке будут непрерывными.

Следующим шагом является проверка результатов. Это делается в два этапа. Первый — построить каждый сегмент по всей длине. Мы ищем четыре граничных условия, которые должны быть выполнены. Как видите, линии пересекаются и касаются друг друга на расстоянии 50 дюймов. Кроме того, v ₁ не имеет прогиба или наклона в основании.

Наконец, мы объединим два графика вместе, образуя окончательное уравнение для отклонения нашей консольной балки. 4.

Теперь определим момент и проинтегрируем уравнение отклонения балки дважды каждый раз, добавляя переменную. Я выбрал две системы координат. Координата x идет слева направо и координата y идет справа налево. Их связывает:

г = L-x

Я выбрал эту систему координат, чтобы C ₂ и C ₄ будут сокращаться, когда мы решаем граничные условия 1 и 2. Это также упрощает математические вычисления. чрезвычайно.Вы увидите через секунду.

Мне нужно выполнить интегрирование только для одного из разделов, а затем изменить I ₁ на I ₂ и w ₁ на w ₂ в уравнениях. В уравнениях правого сечения я также заменю «y» на «x». Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные.

Теперь, когда проблема определена, давайте установим граничные условия.Нам нужно, чтобы концы балки были отклонены на 0 дюймов (BC 1 и 2). Также нам понадобятся еще два граничных условия на стыке сегментов. Наклон и положение в этой позиции должны быть такими же, как и в месте соединения сегментов.

Решим граничные условия 1 и 2

Как упоминалось выше, я предвидел, что переменные C ₂ и C ₄ будет равно 0, если я выберу координату система запускается на базе.

Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее.

Обратите внимание на проверку, которую я вставил в блок поиска, чтобы чтобы мы могли проверить, что v ₁ = v ₂ и s ₁ = с ₂ при 200 дюйм. Это подтверждает что положение и наклон в этой точке будут непрерывными.

Следующим шагом является проверка результатов. Это делается в два этапа. Первый — построить каждый сегмент по всей длине.Мы ищем четыре граничных условия, которые должны быть выполнены.

Ой, что случилось !? Линии определенно пересекаются на расстоянии 200 дюймов, и каждый конец имеет 0 дюймов. прогиб, но они не касаются на пересечении. Я не только показываю силу график решения для точности, но также демонстрируя, что с помощью двух разные системы координат создают проблему. Согласно уравнениям склоны приближаются к месту расположения стык на равном по величине нисходящем склоне.Однако сделать эту работу одной из склонов на самом деле нужно подойти. Мы можем исправьте эту проблему, внеся одно небольшое изменение.

с ₁ = -s ₂

Давайте внесем это изменение и приступим к решению.

Да, намного лучше! Наконец, мы объединим два графика вместе, образуя окончательное уравнение для отклонения нашей консольной балки.

Как и ожидалось, более длинная и жесткая часть меньше прогибается.

Пример 3: Постоянно изменяющаяся неразрезная балка с простой опорой и постоянной распределенной нагрузкой.

Эта проблема состоит из стальной балки с простой опорой длиной 300 дюймов и распределенной нагрузки 1000 фунтов / дюйм поперек балки. Сечение начинается на высоте 10 дюймов, линейно увеличивается к центру, где достигает высоты 24 дюйма. Затем он снова сужается до 10 дюймов.

Чтобы определить, как момент инерции изменяется по отношению к x, мы будем моделировать в Solidworks и делать сечения каждые 30 дюймов. Мы сведем эти данные в таблицу и подгоним к ним линию.

Теперь вы, наверное, заметили, что я сделал таблицу только для значений от 0 до 150 дюймов. Это потому, что я собираюсь использовать симметрию, чтобы упростить эту сложную задачу. Мы можем использовать симметрию, потому что и нагрузка, и сечение балки симметричны относительно середины балки. Из-за симметрии нам нужно, чтобы конечная точка имела прогиб 0 дюймов, а наклон в середине балки был 0 градусов. Затем мы можем отразить это, чтобы получить непрерывное отклонение луча. В этом случае координата x будет идти слева направо.

Здесь вы можете видеть, что вычисленные значения I (x) точно соответствуют тому, что указано в таблице выше. Я назвал вторую производную от положения «а1» (ускорение). Как видите, верхняя и нижняя части имеют переменную «x», и интегрировать это будет очень весело. Итак, вам нужно знать обо мне одну вещь. У меня есть ограничения на то, что я не буду делать. Интеграция — одна из таких вещей. Вот почему у нас есть MathCAD!

Как видите, очень утомительная работа по интеграции была замалчена, и мы смогли напрямую решить для нашей границы условия.В уравнениях s (x) и v (x), на самом деле были натуральные бревна и каким-то образом появилась обратная касательная (не показано). Я до сих пор не жалею позволяя MathCAD делать всю работу.

Следующим шагом является проверка результатов. Это делается в два этапа. Первый — построить каждый сегмент по всей длине. Мы ищем, чтобы наши граничные условия были выполнены. Как видите, отклонение при x = 0 дюймов составляет 0 дюймов, а наклон кажется плоским при x = 150 дюймов.

Наконец, мы отразим графики вместе, образуя окончательное уравнение для отклонения нашей консольной балки.

Как видите, отклонение составляет 0 дюймов в конечных точках и имеет максимальное отклонение в центре.

Заключение

В этой статье рассматриваются три популярных варианта нагружения, когда балка имеет переменное поперечное сечение. Хотя это действительно связано с исчислением, часто это очень легко сделать вручную, потому что это многочлены. Если нет, то будьте благодарны за такие надежные программы, как MathCAD, которые сделают это за вас. Эта статья должна дать вам хорошее представление о процедуре, используемой для анализа подобных балок.Если ваша балка не загружена именно так, вы всегда можете найти расчет момента в таблице и интегрировать свое сердце.

Связанные

Расчет напряжения изгиба секции балки

Как рассчитать напряжение изгиба в балках?

В этом руководстве мы рассмотрим, как рассчитать изгибающее напряжение балки, используя формулу изгибающего напряжения, которая связывает распределение продольных напряжений в балке с внутренним изгибающим моментом, действующим на поперечное сечение балки.Мы предполагаем, что материал балки линейно-упругий (т.е. применим закон Гука). Напряжение изгиба важно, и, поскольку изгиб балки часто является определяющим результатом при проектировании балки, это важно понимать.

1. Расчет напряжения изгиба вручную

Давайте посмотрим на пример. Рассмотрим двутавровую балку, показанную ниже:

На некотором расстоянии по длине балки (ось x) она испытывает внутренний изгибающий момент (M), который обычно можно найти на диаграмме изгибающего момента.Общая формула для изгиба или нормального напряжения в сечении:

Для конкретного сечения балки очевидно, что напряжение изгиба будет максимальным на расстоянии от нейтральной оси (y). Таким образом, максимальное напряжение изгиба будет возникать либо в ВЕРХНЕ, либо в НИЖНЕЙ части секции балки, в зависимости от того, какое расстояние больше:

Давайте рассмотрим реальный пример нашей двутавровой балки, показанной выше. В нашем предыдущем уроке по моменту инерции мы уже обнаружили, что момент инерции относительно нейтральной оси равен I = 4.74 × 10 ⁸ мм ⁴ . Кроме того, в учебнике по центроиду мы обнаружили, что центроид и, следовательно, расположение нейтральной оси находятся на расстоянии 216,29 мм от нижней части секции. Это показано ниже:

Очевидно, что очень часто требуется МАКСИМАЛЬНОЕ напряжение изгиба, которое испытывает секция. Например, предположим, что мы знаем из нашей диаграммы изгибающего момента, что балка испытывает максимальный изгибающий момент 50 кН-м или 50 000 Нм (преобразование единиц изгибающего момента).

Затем нам нужно определить, находится ли верх или низ секции дальше всего от нейтральной оси. Ясно, что нижняя часть секции находится дальше на расстоянии c = 216,29 мм. Теперь у нас достаточно информации, чтобы найти максимальное напряжение, используя приведенную выше формулу напряжения изгиба:

Точно так же мы можем найти напряжение изгиба в верхней части секции, так как мы знаем, что оно составляет y = 159,71 мм от нейтральной оси (NA):

Последнее, о чем следует беспокоиться, это то, вызывает ли напряжение сжатие или растяжение волокон секции.Если балка прогибается в форме буквы «U», то верхние волокна испытывают сжатие (отрицательное напряжение), а нижние волокна — растяжение (положительное напряжение). Если балка провисает, как перевернутая буква «U», то все наоборот: нижние волокна сжимаются, а верхние — растянуты.

2. Расчет напряжения изгиба с использованием балки SkyCiv

Конечно, вам не нужно делать эти расчеты вручную, потому что вы можете использовать SkyCiv Beam — калькулятор напряжения изгиба, чтобы определить напряжение сдвига и изгиба в балке! Просто начните с моделирования балки с опорами и приложения нагрузок.Как только вы нажмете «Решить», программа покажет максимальные напряжения из этого калькулятора напряжения изгиба. На изображении ниже показан пример двутавровой балки, испытывающей напряжение изгиба:

Начните расчет напряжения изгиба с помощью SkyCiv Beam Calculator:

Бесплатный калькулятор луча

Механика материалов: изгиб — нормальное напряжение »Механика тонких конструкций

---

Моменты области

Чтобы рассчитать напряжение (и, следовательно, деформацию), вызванное изгибом, нам нужно понять, где находится нейтральная ось балки и как рассчитать второй момент площади для данного поперечного сечения.

Начнем с представления произвольного поперечного сечения — чего-то не круглого, не прямоугольного и т. Д.

На изображении выше произвольная форма имеет область, обозначенную A . Мы можем посмотреть на небольшую дифференциальную область dA , которая существует на некотором расстоянии x и y от начала координат. Мы можем посмотреть на первый момент площади в каждом направлении по следующей формуле:

Первый момент площади — это интеграл длины по площади — это означает, что единицы длины будут кубическими [L ³ ].Это важно, потому что помогает нам определить центр тяжести объекта. Центроид определяется как «среднее положение области x (или y )». Математически это утверждение выглядит так:

Крайняя правая часть приведенных выше уравнений будет очень полезна в этом курсе — она ​​позволяет нам разбить сложную форму на простые формы с известными площадями и известными положениями центра тяжести. В большинстве инженерных сооружений есть как минимум одна ось симметрии — и это позволяет нам значительно упростить поиск центроида. Центроид должен располагаться на оси симметрии . Например:

Для поперечного сечения слева мы знаем, что центроид должен лежать на оси симметрии, поэтому нам нужно только найти центроид по оси y . Поперечное сечение справа еще проще — поскольку центр тяжести должен совпадать с осями симметрии, он должен находиться в центре объекта.

Теперь, когда мы знаем, как найти центроид, мы можем обратить внимание на второй момент площади.Как вы могли вспомнить из предыдущего раздела, посвященного кручению, это определяется как:

И, наконец, иногда нам нужно определить второй момент площади относительно произвольной оси x или y — такой, который не соответствует центроиду. В этом случае мы можем использовать теорему о параллельных осях для его вычисления. В этом случае мы используем второй момент площади относительно центроида плюс член, который включает расстояния между двумя осями.

Это уравнение называется теоремой о параллельной оси .Это будет очень полезно на протяжении всего курса. Как описано во вводном видео к этому разделу, вычислить второй момент площади для простой формы может быть несложно. Для более сложных форм нам нужно вычислить I , вычислив отдельные I для каждой простой формы и комбинируя их вместе с помощью теоремы о параллельных осях.

Диаграммы сдвига и момента

Поперечная нагрузка относится к силам, перпендикулярным длинной оси конструкции.Эти поперечные нагрузки вызовут изгибающий момент M , который вызывает нормальное напряжение , и силу сдвига V , которая вызывает напряжение сдвига . Эти силы могут изменяться и будут изменяться по длине балки, и мы будем использовать диаграммы сдвига и момента (V-M-диаграмма) , чтобы извлечь наиболее подходящие значения. Построение этих диаграмм должно быть вам знакомо по статике , но мы рассмотрим их здесь. При исследовании поперечно нагруженной балки необходимо учитывать два важных момента:

1. Как нагружается балка?

• точечная нагрузка, распределенная нагрузка (равномерная или переменная), сочетание нагрузок…

1. Как поддерживается балка?

• просто поддерживаемые, консольные, нависающие, статически неопределимые…

Знание нагрузок и опор позволит вам нарисовать качественную диаграмму V-M , а затем статический анализ свободного тела поможет вам определить количественное описание кривых.Начнем с того, что вспомним наши условные обозначения .

Эти правила знаков должны быть вам знакомы. Если сдвиг вызывает вращение против часовой стрелки, он положительный. Если момент изгибает балку таким образом, что он изгибается в «улыбку» или U-образную форму, это положительно. Лучший способ вспомнить эти диаграммы — это проработать пример. Начните с этой консольной балки — отсюда вы можете переходить к более сложным нагрузкам.

Нормальное напряжение при изгибе

Во многом изгиб и кручение очень похожи.Изгиб происходит от пары или прилагаемого изгибающего момента M . Как и при кручении, при чистом изгибе в материале существует ось, на которой напряжение и деформация равны нулю. Это называется нейтральной осью . И, как и при кручении, напряжение перестает быть равномерным по поперечному сечению конструкции — оно меняется. Давайте начнем с рассмотрения того, как ось z изгибает конструкцию. В данном случае мы не будем ограничиваться круговыми сечениями — на рисунке ниже мы будем рассматривать призматическое сечение.

Прежде чем мы углубимся в математику, лежащую в основе изгиба, давайте попробуем разобраться в этом концептуально. Возможно, лучший способ увидеть, что происходит, — это наложить изогнутую балку поверх исходной прямой балки.

Теперь вы можете заметить, что нижняя поверхность балки стала длиннее, а нижняя поверхность балки стала короче. Кроме того, по центру балки длина вообще не изменилась — соответствует нейтральной оси. Чтобы повторить это на языке этого класса, мы можем сказать, что нижняя поверхность находится под напряжением, а верхняя поверхность находится под давлением.Что-то более тонкое, но все же можно наблюдать из наложенного выше изображения, это то, что смещение луча изменяется линейно сверху вниз, проходя через ноль на нейтральной оси. Помните, это именно то, что мы видели и с кручением — напряжение линейно изменялось от центра к центру. Мы можем посмотреть на это распределение напряжений в поперечном сечении балки более подробно:

Теперь мы можем найти математическую связь между приложенным моментом и напряжением в балке.Мы уже упоминали, что балка линейно деформируется от одного края к другому — это означает, что деформация в направлении x увеличивается линейно с расстоянием по оси y- (или по толщине балки). Таким образом, деформация будет максимальной при растяжении при y = -c (поскольку y = 0 находится на нейтральной оси, в данном случае в центре балки), и будет максимальной при сжатии при y = c. . Мы можем записать это математически так:

Теперь это говорит нам кое-что о деформации, что мы можем сказать о максимальных значениях напряжения? Что ж, давайте начнем с умножения обеих частей уравнения на E , модуль упругости Юнга.Теперь наше уравнение выглядит так:

Используя закон Гука, мы можем связать эти величины со скобками под ними с напряжением в направлении x и максимальным напряжением. Это дает нам это уравнение для напряжения в направлении x- :

Наш последний шаг в этом процессе — понять, как изгибающий момент соотносится с напряжением. Для этого напомним, что момент — это сила, умноженная на расстояние. Если мы можем представить себе, что смотрим только на очень маленький элемент в балке, дифференциальный элемент, то мы можем записать это математически как:

Поскольку в нашем уравнении есть дифференциалы, мы можем определить момент M , действующий по площади поперечного сечения балки, интегрировав обе части уравнения.И, если мы вспомним наше определение напряжения как силы, приходящейся на площадь, мы можем написать:

Последний член в последнем уравнении — интеграл по квадрату y — представляет второй момент площади относительно оси z (из-за того, как мы определили наши координаты). В декартовых координатах этот второй момент площади обозначается как I (помните, в цилиндрических координатах он обозначался как J ). Теперь мы можем, наконец, записать наше уравнение для максимального напряжения и, следовательно, напряжения в любой точке вдоль оси y , как:

Важно отметить, что индексы в этом уравнении и направление вдоль поперечного сечения (здесь оно измеряется вдоль и ) все будут меняться в зависимости от характера проблемы, т.е.е. направление момента — вокруг какой оси изгибается балка? Мы основали наши обозначения на показе изогнутой балки на первом изображении этого урока.

Помните, в начале раздела я упоминал, что изгиб и кручение на самом деле очень похожи? На самом деле мы очень явно видим это в последнем уравнении. В обоих случаях напряжение (нормальное для изгиба и сдвиг для кручения) равно пара / момент ( M для изгиба и T для кручения), умноженному на местоположения вдоль поперечного сечения. , , потому что напряжение неравномерно по поперечному сечению (с декартовыми координатами для изгиба и цилиндрическими координатами для кручения), все деленное на секундный момент площади поперечного сечения.

Сводка

В этом уроке мы узнали о моментов области и диаграммах момента сдвига . Из первого момента площади поперечного сечения мы можем вычислить центроид . Мы узнали, как вычислить секундный момент площади в декартовых и полярных координатах, и мы узнали, как теорема о параллельной оси позволяет нам вычислить второй момент площади относительно центроида объекта — это полезно для разделения сложного поперечного сечения на несколько простых форм и объединение их вместе.Мы пересмотрели концепцию диаграмм сдвига и момента из статики. Эти диаграммы будут важны для определения максимальной силы сдвига и изгибающего момента вдоль сложно нагруженной балки, которые, в свою очередь, потребуются для расчета напряжений и прогнозирования разрушения. Наконец, мы узнали о нормальном напряжении при изгибе балки. И напряжение, и деформация изменяются вдоль поперечного сечения балки, при этом одна поверхность находится в состоянии растяжения, а другая — в состоянии сжатия. Плоскость, проходящая через центроид, образует нейтральную ось — вдоль нейтральной оси нет напряжения или деформации.Напряжение является функцией приложенного момента и второго момента площади относительно оси, вокруг которой находится момент.

Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта № 1454153. Любые мнения, выводы, выводы или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национального научного фонда. Научный фонд.

Напряжение балки из-за изгибающих моментов — Приложение по прочности материалов для энергетики

Напряжение изгиба

Цели обучения

После завершения этой главы вы сможете:

• Используйте формулу изгиба для расчета максимального напряжения изгиба
• Расчетные балки, безопасно несущие нагрузки
• Определите требуемый модуль упругости сечения балки
• Выбор стандартных структурных форм для использования в данной задаче балки

Рассмотрим балку с простой опорой, подверженную внешним нагрузкам, направленным вниз.Балка будет деформироваться (отклоняться) таким образом, что верхняя поверхность поперечного сечения балки будет испытывать сжатие, а нижняя поверхность — растяжение. В некотором месте вдоль вертикальной оси балки напряжение будет нулевым; это место является центром тяжести поперечного сечения, также называемым нейтральной осью.

Формула изгиба

Для определения максимального напряжения из-за изгиба используется формула изгиба :

где:

• σ _max — максимальное напряжение на самой удаленной от нейтральной оси поверхности (может быть верхней или нижней)
• M — изгибающий момент по длине балки, где рассчитывается напряжение
  • если требуется максимальное изгибающее напряжение, то M — максимальный изгибающий момент, действующий на балку
• I _x — момент инерции относительно центральной оси x (горизонтальной)
• c — максимальное расстояние от центральной оси до крайнего волокна (опять же, это может быть верх или низ формы)
• Z _x называется модулем упругости сечения и представляет собой термин, который объединяет момент инерции и расстояние до крайнего волокна ( Z _x = I _x / c )

Формула изгиба действительна при соблюдении следующих критериев:

• балка прямая, относительно длинная и узкая, с равномерным поперечным сечением
• все нагрузки действуют перпендикулярно продольной оси балки
• результирующее напряжение ниже предела пропорциональности материала
• материал балки однороден и имеет равную прочность на растяжение и сжатие.
  • , если материал имеет разную прочность на растяжение и сжатие (например, чугун или другие анизотропные материалы), тогда требуются отдельные расчеты как для поверхностей растяжения, так и для поверхностей сжатия
• нет скручивания, коробления или деформации

Дизайнерские корпуса

Проблемы проектирования могут возникать по разным сценариям:

• рассчитать размеры поперечного сечения балки (найти минимальный модуль сечения Z и выбрать стандартную форму с большей жесткостью) с учетом геометрии балки, нагрузки и материала.
• выберите материал балки (найдите максимальное рабочее напряжение и выберите материал большей прочности) с учетом размеров балки, нагрузки и размеров / формы.
• определяет, является ли балка безопасной (найдите фактическое рабочее напряжение и сравните с расчетным напряжением), учитывая размеры балки, нагрузку и материал.

Назначенные задачи

Примечание: если не указано иное, используйте конструкцию = 0,6 × σ _YS, , где σ _YS — предел текучести, из учебного приложения B.

Задача 1: Балка с простой опорой длиной 9,9 м нагружается сосредоточенными нагрузками следующим образом:

• 40 кН на расстоянии 1,2 м от левого края
• 10 кН на расстоянии 3,7 м от левого края
• 10 кН на расстоянии 6,2 м от левого края
• 10 кН на расстоянии 8,7 м от левого края

Балка изготовлена ​​из двутаврового профиля W200 × 100 из холоднокатаного материала AISI-1020. AISC рекомендует, чтобы максимальное напряжение изгиба для строительных конструкций при статических нагрузках было ниже 0.66 × S _y . Соответствует ли эта конструкция проектным требованиям?

Задача 2: Трубопровод просто поддерживается над землей на горизонтальных балках длиной 4,5 м. Каждая балка несет вес 20 м трубы Sch 40 DN-600 (см. PanGlobal Academic Extract), заполненной маслом 0,9 SG . Предполагая, что нагрузка действует в центре балки, рассчитайте необходимый модуль упругости балки, чтобы ограничить изгибающее напряжение до 140 МПа; затем выберите самый легкий W-луч SI, который удовлетворяет критериям.

Задача 3: На рисунке показано поперечное сечение балки из алюминия 6061-T6. Балка используется как консоль длиной 45 дюймов. Вычислите максимально допустимую равномерно распределенную нагрузку, которую он может выдержать при ограничении напряжения из-за изгиба до одной пятой от предельной прочности.

Задача 4: Спроектируйте проход, чтобы перекрыть только что проложенный трубопровод на вашем предприятии. Жесткие опоры доступны с каждой стороны трубопровода на расстоянии 14 футов друг от друга.Тротуар должен иметь ширину 3,5 фута и выдерживать равномерно распределенную нагрузку 60 фунтов / фут ² по всей своей поверхности. Проектируйте только доски настила и боковые балки. Используйте древесину любых размеров и сортов материала из Приложения E к учебникам или других материалов, разработанных вами.

Задача 5: Предложите одну проблему конструкции балки, которую вы сочтете актуальной и полезной для инженеров-энергетиков.

---

ЧАСТЬ ТРЕТЬЯ

---

ИЗгиб балок с несимметричным сечением

Большинство конструктивных элементов самолета состоит из балок с несимметричной крестовиной. сечение, действующее при изгибе.По этой причине необходимо получить выражение, позволяющее определять напряжения, создаваемые изгибающими моментами в таких секциях.

ЗНАК ОБОЗНАЧЕНИЯ И ОБОЗНАЧЕНИЯ

Посмотрите на систему осей Oxyz с произвольным лучом, параллельным оси z:

Рис. 8: Обозначения и условные обозначения для положительных сил, моментов и перемещений.

Где:

T = крутящий момент

M = изгибающий момент

S = поперечная сила

w

= Распределенная нагрузка

P = Осевая или прямая нагрузка

u, v, w = осевые смещения

Все эти внешние нагрузки положительны в направлении, указанном на рисунке. Внутренний момент и силы, приложенные к грани A, имеют то же направление и направление, что и внешнее приложение. нагрузки.Однако на грани B положительные внутренние моменты и силы противоположны.

РАЗРЕШЕНИЕ ИЗГИБНЫХ МОМЕНТОВ

Изгибающий момент M, приложенный в любой плоскости, параллельной оси z, может быть разделен на компоненты M _x и M _y по правилам вектора нормали.

Сделав это визуально, будет легче увидеть:

Рис. 9: Разрешенный изгибающий момент относительно осей x и y.

Из рисунка 9 можно получить следующие соотношения:

M _x = M sin θ

M _y = M cos θ

и что эти моменты могут иметь разный знак в зависимости от значения θ. Например, если θ> π / 2, M _x положительно, а M _y отрицательно.

РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ (ETB-NonSym)

Рассмотрим балку произвольного несимметричного поперечного сечения, которая поддерживает изгибающие моменты Mx и My, изгибающуюся вокруг некоторой оси в поперечном сечении.Это плоскость без напряжения изгиба, называемая нейтральной осью (N.A.).

Рисунок 10: Определение положения нейтральной оси.

Пусть начало оси совпадает с центром тяжести G поперечного сечения, а нейтральная ось находится на расстоянии p от G.

Прямое напряжение s _z на элементе d _A в точке (x, y) и на расстоянии x от нейтральной оси составляет:

Посмотрите на балку в плоскости, параллельной нейтральной оси, с двумя сегментами ij и kl , которые имеют одинаковую длину, когда балка не отклонена:

Рис. 11: Вид сбоку неотклоненной балки с сегментами ij и kl отмечены.

После отклонения луча это сечение будет выглядеть так:

Рисунок 12: Отклоненная балка.

где:

R = радиус кривизны

dq = угол между плоскостями ik и jl

Деформация в плоскости kl может быть определена как:

с

и

дает

Подставляя обратно в уравнение напряжений, получаем:

(3.2)

Теперь, когда уравнение напряжений получено, необходимо обеспечить как вращательное, так и линейное равновесие на концах балки. То есть сумма сил по глубине балки равна «0», а сумма моментов по глубине балки равна приложенным моментам Mx и My.

Поскольку балка поддерживает чистый изгиб, результирующая нагрузка на концевую секцию должна быть нулевой. Следовательно,

Подставляя уравнение 3.2 дает:

Это уравнение определяет положение центроида сечения, из которого следует, что нейтральная ось должна проходить через центроид.

Вместо того, чтобы использовать это уравнение для определения местоположения центроида, гораздо проще определить местоположение центроида вокруг оси xy с помощью уравнения 3.3.

Для достижения равновесия моментов необходимо заново нарисовать рисунок 10, но с осью, проходящей через центроид.

Рисунок 13: Сечение балки с нейтральной осью, проходящей через центроид.

Чтобы увидеть это более подробно, на рисунке 14 крупным планом показана ось и область dA .

Рисунок 14: Деталь площади dA в поперечном сечении балки.

Если наклон нейтральной оси (N.A.) находится под углом к ​​оси x, то:

x

= x sin α + y cos α (3,4)

и замена в 3.2 дает:

(3,5)

Результирующие момента имеют тот же смысл, что и приложенные моменты, отсюда:

, г. (3,6)

и подставив уравнение 3.4 в уравнения 3.5 дает:

и

Члены sin α и cos α не являются функцией dA, поэтому их можно исключить из интегрирования. Остались термины, которые имеют отношение только к характеристикам форм поперечного сечения балки, а это всего лишь 2 момента ^и площади балки.

Вторые моменты области вокруг осей xy:

, что дает:

решение одновременно дает,

Подставляя в уравнение (3.5) дает:

Определив термины Эффективный изгибающий момент , как:

и

Уравнение 3.8 можно переписать следующим образом:

Обратите внимание на , что если луч симметричен относительно оси x или оси y, то:

, а оси x и y — это основные оси .

ПОЛОЖЕНИЕ НЕЙТРАЛЬНОЙ ОСИ

Местоположение нейтральной оси определялось уравнением (3.3) .

Для балки с симметричным поперечным сечением центр тяжести — это точка, определяемая уравнением 3.3, а нейтральная ось параллельна осям x и y. Для несимметричного балочного креста Однако нейтральная ось проходит под некоторым углом a по отношению к оси x. Что нужно сделать, определите угол нейтральной оси.

В N.A. нормальные изгибающие напряжения равны s _z = 0, что дает:

где:

x _Н.A. и y _N.A. — координаты точек вдоль нейтральной оси, что дает:

Взяв величину, обратную тангенту угла «a», можно найти угол нейтральной оси по отношению к оси x, задаваемый уравнением 3.12.

Пример 1: Показанная балка подвергается изгибающему моменту 150 Нм вокруг оси x. Рассчитайте максимальное прямое напряжение из-за изгиба, указав, где оно действует.

Рис. 15: Поперечное сечение балки с приложенным изгибающим моментом.

а) Определите положение центроида относительно точки A а также

б) Сдвинуть ось к центроиду

Рис. 16: Поперечное сечение балки со смещением оси в положение центра тяжести.

c) Определение других свойств сечения

d) Расчет эффективных изгибающих моментов

Поскольку M _x = 1500 и M _y = 0, подстановка этих значений в уравнения (3.9) и (3.10) дает:

e) Определить уравнение напряжения изгиба и напряжения поперечного сечения

Подставьте вычисленные выше значения в уравнение (3.11) .

Подставив координаты всех угловых точек из рисунка 16, получим:

Пункт	x (мм)	y (мм)	с z (МПа)
1	72	21,6	0,436
2	-48	21.6	5,1
3	-48	13,6	3,9
4	-16	13,6	2,66
5	-16	-66,4	-9,32
6	-8	-66,4	-9,63
7	-8	13.6	2,34
8	72	13,6	-0,76

Этот метод можно использовать для определения напряжений из-за изгиба в балке любого типа с любым типом поперечного сечения.

ПРИБЛИЖЕНИЕ ДЛЯ ТОНКОСТЕННЫХ ПРОФИЛЕЙ

Из-за тонкости конструкции самолета можно сделать предположение, что напряжения постоянны на всей толщине t обшивки.Сказав это, квадрат и более высокие степени t можно не учитывать при вычислении свойств сечения.

Чтобы увидеть это, посмотрите раздел каналов:

Рисунок 17: Секция тонкостенного канала.

1) Поскольку сечение симметрично относительно оси x, то I _xy = 0 2) Второй момент площади I _xx определяется как: Расширение RHS дает:

за счет исключения t ² степеней и выше он становится:

и аналогично

Это указывает на то, что свойства сечения могут быть рассчитаны так, как если бы сечение было представлено тонкой линией, как показано на рисунке 18, без учета любых t ² или более высоких членов.

Рисунок 18: Приближение сечения канала.

Для этого дискретного тонкостенного профиля характеристики сечения будут следующими:

1) Определите местоположение центроида

2) Сдвинуть ось к центроиду

Рисунок 19: Ось в центре тяжести

3) Определение моментов инерции

Эти результаты точно такие же, как и для сечения с учетом толщины материала обшивки и без учета всех членов t ² и выше.

Поскольку не все участки кожи будут лежать параллельно оси x или y, локальные моменты или площадь участка кожи под углом q по отношению к оси x задаются следующими уравнениями.

Рис. 20: Тонкий участок кожи, наклоненный под углом θ относительно оси x

ОБЩИЕ ОТНОШЕНИЯ ПО НАГРУЗКЕ

Рассмотрим элемент длиной dz из балки с несимметричным поперечным сечением со всеми видами нагрузок, приложенных в плоскости y-z, рисунок 21.

Рисунок 21: Равновесие обычно нагруженного элемента балки в плоскости zy.

Равновесие элемента в направлении y дает:

делением на dz и в пределе dz0 это уравнение упрощается до:

Рассмотрение моментов об А дает:

делением на dz и в пределе dz0 это уравнение упрощается до:

Объединение этих двух уравнений дает:

Точно так же про плоскость x-z:

Теперь рассмотрим элемент длиной dz из балки с несимметричным поперечным сечением только с приложенным крутящим моментом вокруг оси z, рисунок 22.

Рисунок 22: Уравновешивание крутящего момента секции балки длиной dz.

Принимая моменты относительно оси Z:

делением на δz и в пределе δz0 это уравнение упрощается до:

Предполагая, что параметр имеет такое же отношение к , как S _y имеет к M _x , тогда путем дифференцирования уравнений (3.9) и (3.10) дает:

Также параметры и связаны с интенсивностями нагрузки w _y и w _x таким же образом, что путем дифференцирования уравнений (3.16) и (3.17) дает:

Параметры ,, и называются ЭФФЕКТИВНЫЕ СДВИГАТЕЛЬНЫЕ СИЛЫ и ИНТЕНСИВНОСТЬ НАГРУЗКИ .

… В начало

% PDF-1.5 % 885 0 объект > эндобдж xref 885 85 0000000016 00000 н. 0000003220 00000 н. 0000003370 00000 н. 0000003941 00000 н. 0000004078 00000 н. 0000004210 00000 н. 0000004349 00000 п. 0000004491 00000 н. 0000004518 00000 н. 0000005188 00000 п. 0000005398 00000 п. 0000005959 00000 н. 0000006156 00000 н. 0000006193 00000 п. 0000006768 00000 н. 0000006880 00000 н. 0000006994 00000 н. 0000007207 00000 н. 0000007603 00000 н. 0000008080 00000 н. 0000008107 00000 н. 0000008134 00000 п. 0000008630 00000 н. 0000009382 00000 п. 0000009894 00000 н. 0000010605 00000 п. 0000011298 00000 п. 0000012005 00000 п. 0000012138 00000 п. 0000012287 00000 п. 0000012314 00000 п. 0000012808 00000 п. 0000012835 00000 п. 0000013255 00000 п. 0000013946 00000 п. 0000014608 00000 п. 0000015271 00000 п. 0000015356 00000 п. 0000036914 00000 п. 0000037207 00000 п. 0000037606 00000 п. 0000037692 00000 п. 0000079126 00000 п. 0000079409 00000 п. 0000079979 00000 п. 0000080049 00000 п. 0000080119 00000 п. 0000080200 00000 п. 0000087193 00000 п. 0000087455 00000 п. 0000087721 00000 п. 00000 00000 п. 00000 00000 п. 00000 _{00000 п. 00000 00000 п. 0000112939 00000 н. 0000113208 00000 н. 0000113638 00000 н. 0000113708 00000 н. 0000133265 00000 н. 0000133528 00000 н. 0000139507 00000 н. 0000139895 00000 н. 0000139965 00000 н. 0000140002 00000 н. 0000140072 00000 н. 0000140153 00000 н. 0000146096 00000 н. 0000146367 00000 н. 0000146535 00000 н. 0000146562 00000 н. 0000146860 00000 н. 0000146966 00000 н. 0000148830 00000 н. 0000149138 00000 н. 0000149488 00000 н. 0000149587 00000 н. 0000150975 00000 н. 0000151277 00000 н. 0000151617 00000 н. 0000154202 00000 н. 0000155641 00000 н. 0000158226 00000 н. 0000003021 00000 н. 0000002037 00000 н. трейлер ] / Назад 834216 / XRefStm 3021 >> startxref 0 %% EOF 969 0 объект > поток hb«b`b`g«db @}

Расчет прочности двутавровой балки на прочность

Расчет расчетной прочности двутавровой балки для расчета нормальное напряжение, напряжение сдвига и напряжение фон Мизеса в критических точках данного сечение двутавра.

Поперечная нагрузка на двутавровую балку может привести к нормальным напряжениям и напряжениям сдвига. одновременно на любом поперечном сечении двутавра. Нормальное напряжение на данном поперечном сечении изменяется относительно расстояние y от нейтральной оси, и оно наибольшее в самой дальней точке от нервная ось. Нормальное напряжение также зависит от изгибающего момента в сечение и максимальное значение нормального напряжения в двутавровой балке возникает там, где изгибающий момент наибольший.Максимальное напряжение сдвига возникает на нейтральной оси двутавровой балки, где сила сдвига максимальна.

Примечание. Для получения дополнительной информации о см. разделы «Напряжения сдвига в тонкостенных элементах» и «Конструкция балок и валов на прочность »главы механики материалов .

Примечание: V и M — поперечная сила и изгибающий момент в сечении, как показано на фигура. 4 Расчет напряжений на участке A МПапсикси Нормальное напряжение [σ _{x_A} ] — Напряжение сдвига [τ _{xy_A} ] — Напряжение по Мизесу при A [σ _{v_A} ] — Расчет напряжений на участке B Нормальное напряжение при B [σ _{x_B} ] — Напряжение сдвига при B [τ _{xy_B} ] — Напряжение фон Мизеса при B [σ _{v_B} ] — Расчет напряжений на участке D Нормальное напряжение при D [σ _{x_D} ] — Напряжение сдвига при D [τ _{xy_D} ] — Напряжение по Мизесу при D [σ _{v_D} ] —

Примечание: используйте точку «.»как десятичный разделитель.

Примечание. Напряжения являются положительными числами, и это величины напряжений в луч. Он не делает различий между растяжением и сжатием конструкции. луч.

Примечание: Эффекты концентраций напряжений не учитываются в расчетах.

Двутавровая балка: Двутавровая балка — разновидность балки. часто используется в фермах в зданиях.Двутавровая балка обычно изготавливается из конструкционные стали, подвергнутые горячей и холодной прокатке или сварке. Верхняя и нижняя пластины двутавровой балки называются полками, а вертикальная пластина, соединяющая полки, называется стенкой.

Нормальное напряжение: Напряжение действует перпендикулярно поверхности (поперечному сечению).

Второй момент области: способность поперечного сечения противостоять изгибу.

No related posts.