Расчёт балки бесплатно онлайн

---

Закрыть

Примечание. Иллюстрации в отчёте сформированы шириной в 420px (диалог «Настройки»).

Исходные данные

L = 10м; q = 12кН/м; M = 15кН·м; F = 19кН.

Рис. 1. Исходная схема

Расчёт

Рис. 2. Схема реакций

Рис. 3. Эпюра Qy, кН (поперечная сила)

Рис. 4. Эпюра Mx, кН·м (изгибающий момент)

1. Определение реакций опор

Составим уравнения статического равновесия.

∑F_y = -q·7м — F + Y_A + Y_B = 0;

∑M_A = -q·7м·3.5м + M — F·10м + Y_B·7м = 0.

Решение уравнений статики даёт следующие значения реакций:

Y_A = 36кН;

Y_B = 67кН.

2. Построение эпюр внутренних силовых факторов

Участок №1 (0 ≤ z₁ ≤ 7м)

Q_y = Y_A — q·z₁;

при z₁ = 0; Q_y = 36кН.

при z₁ = 7м; Q_y = -48кН.

M_x = Y_A·z₁ — q·z₁²/2;

при z₁ = 0; M_x = 0.

при z₁ = 3м; M_x = 54кН·м.

при z₁ = 7м; M_x = -42кН·м.

Участок №2 (0 ≤ z₂ ≤ 3м)

Q_y = F = 19кН.

M_x = M — F·z₂;

при z₂ = 0; M_x = 15кН·м.

при z₂ = 3м; M_x = -42кН·м.

Закрыть

---

sopromat.ueuo.com

Расчет опорных реакций балки на двух опорах онлайн

Расчет выполняется по следующей методике:

1. Заменяем распределенную нагрузку ее равнодействующей, которая является сосредоточенной силой. Для равномерно распределенной нагрузки равнодействующая равна произведению интенсивности нагрузки q на длину участка L, на котором она действует: Fq = q*L.

2. Обозначаем опоры. Общепринято их обозначать буквами А и В. Простая балка имеет одну шарнирно-неподвижную и одну шарнирно-подвижную опоры.

3. Освобождаемся от опор и заменяем их действие на балку реакциями.

Реакции опор при такой нагрузке будут только вертикальными.

4. Составляем уравнения равновесия вида:
M_A = 0; M_B = 0,
Моментом силы относительно точки называется произведение этой силы на плечо — кратчайшее расстояние от этой точки приложения силы (в общем случае — до линии действия силы).

5. Выполним проверку решения. Для этого составим уравнение равновесия: Y = 0,
Если оно удовлетворено, то реакции найдены правильно, а если нет, но в решении допущена ошибка.

6. Строим эпюру поперечных сил Q_x. Для этого определяем значения поперечных сил в характерных точках. Напомним, что поперечная сила в сечении равна сумме проекций всех сил, расположенных только слева или только справа от рассматриваемого сечения, на ось, перпендикулярную оси элемента. Силу, расположенную слева от рассматриваемого сечения и направленную вверх, считают положительной (со знаком «плюс»), а направленную вниз — отрицательной (со знаком «минус»). Для правой части балки — наоборот.

В сечениях, соответствующих точкам приложения сосредоточенных сил, в том числе в точках приложения опорных реакций, необходимо определить два значения поперечной силы: чуть левее рассматриваемой точки и чуть правее ее. Поперечные силы в этих сечениях обозначаются соответственно Q_лев и Q_прав.
Найденные значения поперечных сил в характерных точках откладываются в некотором масштабе от нулевой линии. Эти значения соединяются прямыми линиями по следующим правилам:
а) если к участку балки нет распределенной нагрузки, то под этим участком значения поперечных сил соединяются прямой линией, параллельной нулевой линии;
б) если на участке балки приложена распределенная нагрузка, то под этим участком значения поперечных сил соединяются прямой, наклонной к нулевой линии. Она может пересекать или не пересекать нулевую линию.
Соединив все значения поперечных сил по указанным правилам, получим график изменения поперечных сил по длине балки. Такой график называется эпюрой Q

x.

7. Строим эпюру изгибающих моментов М_x. Для этого определяем изгибающие моменты в характерных сечениях. Напомним, что изгибающий момент в рассматриваемом сечении равен сумме моментов всех сил (распределенных, сосредоточенных, в том числе и опорных реакций, а также внешних сосредоточенных моментов), расположенных только слева или только справа от этого сечения. Если любое из перечисленных силовых воздействий стремится повернуть левую часть балки по часовой стрелке, то оно считается положительным (со знаком «плюс»), если против — отрицательным (со знаком «минус»), а для правой части наоборот.
В сечениях, соответствующих точкам приложения сосредоточенных моментов, необходимо определить два значения изгибающего момента: чуть левее рассматриваемой точки и чуть правее ее. Изгибающие моменты в этих точках обозначаются соответственно М

лев и М_прав. В точках приложения сил определяется одно значение изгибающего момента.
Полученные значения откладываются в некотором масштабе от нулевой линии. Эти значения соединяются в соответствии со следующими правилами:
а) если на участке балки нет распределенной нагрузки, то под этим участком балки два соседних значения изгибающих моментов соединяются прямой линией;
б) если к участку балки приложена распределенная нагрузка, то под этим участком значения изгибающих моментов для двух соседних точек соединяются по параболе.

Пример решения балки:

stroydocs.com

Расчет балок онлайн. Примеры расчета

Расчет балки различается в зависимости от того, является она статически определимой, либо статически неопределимой. На сайте производится

расчет любых балок, но подробное решение расписывается только для статически определимых балок, не имеющих промежуточных шарниров.

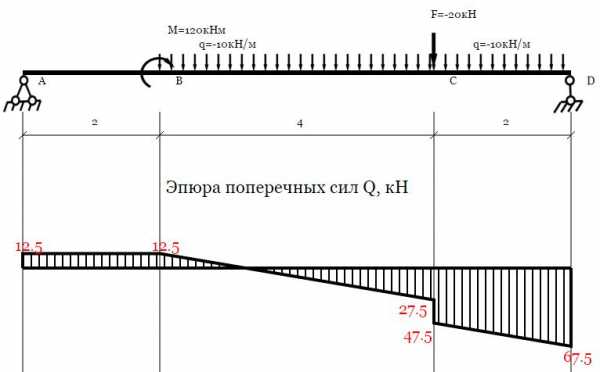
Балка на двух опорах. Построение эпюр

Для этого типа балок сервис позволяет определить и подробно расписывает:

• реакции опор
• эпюры поперечных сил и изгибающих моментов (эпюры Q и M)
• подбор сечений — двутавр, прямоугольник, круг, квадрат, труба
• строятся эпюры нормальных и касательных напряжений
• по уравнениям метода начальных параметров вычисляются прогибы и углы поворота. Записываются и сами уравнения метода начальных параметров по участкам.

Посмотреть пример »

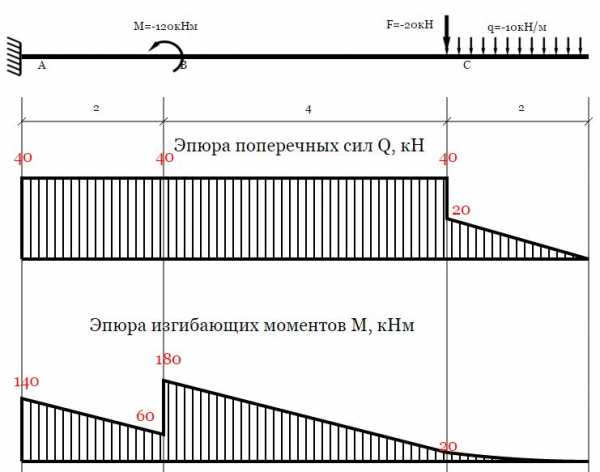
Консольная балка. Построение эпюр.

Для этого типа балок сервис позволяет определить и подробно расписывает:

• построение эпюр поперечных сил и изгибающих моментов
• подбор сечений — двутавр, прямоугольник, круг, квадрат, труба
• строятся эпюры нормальных и касательных напряжений
• вычисляются прогибы и углы поворота.

Посмотреть пример »

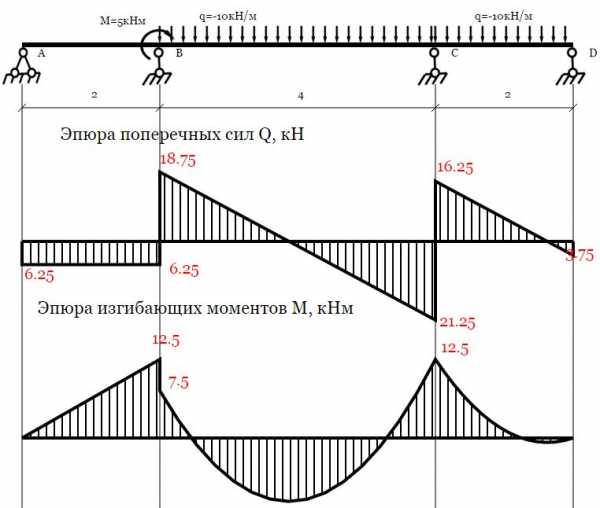
Статически неопределимая балка. Подбор сечения.

Для такого типа балок Вы можете получить

• только результаты расчета — (эпюры Q и M).

Естественно, по этим эпюрам можно легко найти реакции опор. Подробный ход расчета не расписывается, но, имея результаты, Вы легко можете проверить все промежуточные итоги своего расчета.

Посмотреть пример »

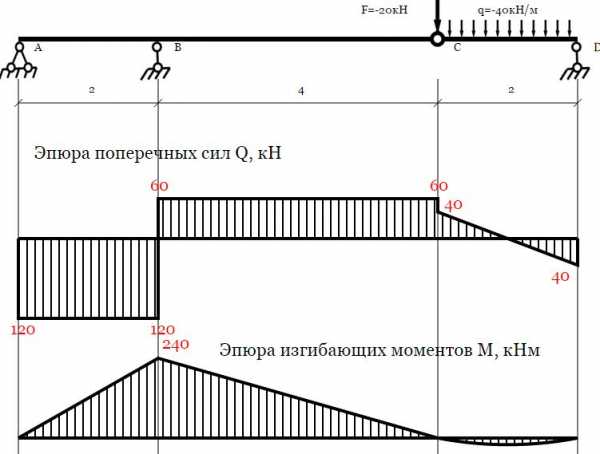
Балка с промежуточными шарнирами

Расчет балки с промежуточными шарнирами Вы должны производить, скорее всего, методом построения поэтажной схемы. Сервис, опять же, дает только конечный результат, но его наличие, естественно, очень упрощает проверку промежуточных этапов решения заданий.

 

Посмотреть пример »

sopromat.xyz

Расчет консольной балки, подбор прямоугольного сечения, эпюры онлайн

Определение опорных реакций

1. Согласно схеме решения задач статики определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки.
2. На балку наложена связь в точке A (справа)  типа жесткая заделка, поэтому освобождаем балку, заменив действие связи реакциями (HA, RA, MA).
3. Определим реакции опор в соответствии с уравнениями равновесия балки: ΣFx = 0, ΣFy = 0, ΣMA = 0.
ΣFx = 0:    HA = 0
ΣFy = 0:    - q1*1 + P1 + RA = 0;
ΣMA = 0:    q1*1*(1.1+1/2) - 1.1*P1 - M1 + MA = 0;
4. Решаем полученную систему уравнений, находим неизвестные : 
HA = 0 (кН)
RA =  q1*1 - P1 =  90*1 - 70 = 20.00 (кН)
MA =  - q1*1*(1.1+1/2) + 1.1*P1 + M1 =  - 90*1*(1.1+1/2) + 1.1*70 + 18 = -49.00 (кН*м), так как момент отрицателен, на расчетной схеме направим его в противоположную сторону.
5. Сделаем проверку, составив дополнительное моментное уравнение отоносительно свободного конца балки: 
- q1*1*(1/2) + 1*P1 - M1 + 2.1*RA - MA =  - 90*1*(1/2) + 1*70 - 18.00 + 2.1*20.00 - 49.00 = 0

Построение эпюр

Рассмотрим 1-й участок 0 ≤ x₁ < 1

Поперечная сила Q:
Q(x1) =  - q1*(x1 - 0)
Значения Q на краях участка:
Q1(0) =  - 90*(0 - 0) = 0 (кН)
Q1(1) =  - 90*1 = -90 (кН)
Изгибающий момент M:
M(x1) =  - q1*(x1)2/2
Значения M на краях участка:
 M1(0) =  - 90*(0 - 0)2/2 = 0 (кН*м)
M1(1) =  - 90*12/2 = -45 (кН*м)

Рассмотрим 2-й участок 1 ≤ x₂ < 1.5

Поперечная сила Q:
Q(x2) =  - q1*1 + P1
Значения Q на краях участка:
Q2(1) =  - 90*1 + 70 = -20 (кН)
Q2(1.50) =  - 90*1 + 70 = -20 (кН)
Изгибающий момент M:
M(x2) =  - q1*1*[(x2 - 1) + 1/2] + P1*(x2 - 1)
Значения M на краях участка:
M2(1) =  - 90*1*(0 + 0.50) + 70*(1 - 1) = -45 (кН*м)
M2(1.50) =  - 90*1*(0.50 + 0.50) + 70*(1.50 - 1) = -55 (кН*м)

Рассмотрим 3-й участок 1.5 ≤ x₃ < 2.1

Поперечная сила Q:
Q(x3) =  - q1*1 + P1
Значения Q на краях участка:
Q3(1.50) =  - 90*1 + 70 = -20 (кН)
Q3(2.10) =  - 90*1 + 70 = -20 (кН)
Изгибающий момент M:
M(x3) =  - q1*1*[(x3 - 1) + 1/2] + P1*(x3 - 1) + M1
Значения M на краях участка:
M3(1.50) =  - 90*1*(0.50 + 0.50) + 70*(1.50 - 1) + 18 = -37 (кН*м)
M3(2.10) =  - 90*1*(1.10 + 0.50) + 70*(2.10 - 1) + 18 = -49 (кН*м)

Прямоугольное сечение балки подбираем из условия прочности при допускаемом напряжении:  = 160 (МПа)

, где:

 — нормальные напряжения, МПа;

 — наибольшее по абсолютной величине значение изгибающего момента, определяемое по эпюре моментов Mx, кН*м;

 — момент сопротивления, см³;

 — допустимое значение нормального напряжения (расчетное сопротивление), МПа;

Момент сопротивления прямоугольного сечения определим по формуле:

Требуемый момент сопротивления определяем по формуле:

Поскольку дано соотношение сторон

Отметим, что полученные размеры являются минимально необходимыми для обеспечения прочности заданной балки. Следовательно, за окончательные размеры прямоугольного сечения балки принимаем: h=165 (мм), b=85 (мм)

Расчет произведен при помощи онлайн-сервиса SOPROMATGURU.RU

sopromatguru.ru