Определение коэффициента гидравлического трения для трубопровода – Коэффициент гидравлического трения
Определение коэффициента гидравлического трения прямой трубы
Министерство образования и науки Российской Федерации
Национальный исследовательский ядерный университет «МИФИ»
Балаковский инженерно-технологический
Методические указания к выполнению лабораторной работы
по дисциплинам: «Гидравлика», «Механика жидкости и газа», «Водоснабжение и водоотведение с основами гидравлики», «Гидрогазодинамика», «Гидравлика и гидропневмопривод»
для студентов направлений: «Теплоэнергетика и теплотехника», «Строительство», «Конструкторско-технологическое обеспечение машиностроительных производств», «Строительство уникальных зданий и сооружений» », «Наземные транспортно-технологические средства»
профиль «Подъемно-транспортные, строительные, дорожные средства и оборудование»
очной, заочной и заочно-сокращенной форм обучения
Балаково 2015
Ц е л ь р а б о т ы:
1.Определить опытным путем коэффициент гидравлического трения.
2.Определить коэффициент гидравлического трения по теоретическим формулам и сравнить с опытным значением.
ОСНОВНЫЕ ПОНЯТИЯ
Потеря напора на трение по длине круглых труб hl oпределятся по формуле Дарси:
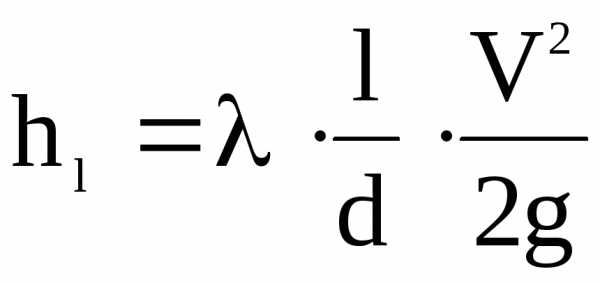 ,
(1)
,
(1)
где — коэффициент гидравлического трения;
l — длина трубы, на которой определяется потеря напора на трение;
d — диаметр трубы ;
V — средняя скорости жидкости;
g — ускорение силы тяжести, равное 981 см/с 2 .
Многочисленными
экспериментами установлено, что
коэффициент гидравлического трения
зависит в общем случае от числа Рейнольдса
Re и относительной шероховатости стенок
трубы  :
:
 ,
(2)
,
(2)
где — высота выступов шероховатости внутренних стенок трубы.
Преобладание того или иного фактора зависит от режима течения жидкости.
Существует пять зон гидравлического сопротивления.
1. З о н а в я з к о г о с о п р о т и в л е н и я.
Движение ламинарное, Re < 2300. В этой зоне шероховатость стенок мало влияет на потери напора
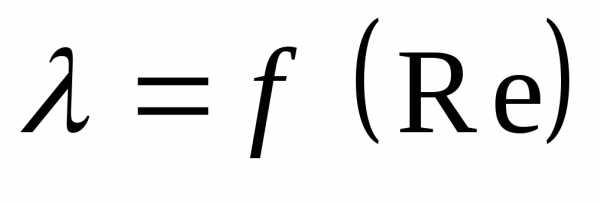 .
(3)
.
(3)
Теоретическая формула для определения коэффициента гидравлического трения для круглой трубы вытекает из закона Пуазейля :
 .
(4)
.
(4)
2. П е р е х о д н а я з о н а. При 2300 < Re < 4000 имеет место переходная зона, в которой движение уже не ламинарное и еще не турбулентное, т. е. здесь режим неустойчивый. Инженерные расчеты в этой зоне выполняются очень редко.
3. З о н а г
и д р а в л и ч е с к и г л а д к
и х т р у б. Движение турбулентное
4000 < Re < 10 5 . В этой зоне шероховатость стенок трубы
мало влияет на потери напора  .
.
Для определения коэффициента гидравлического трения существует множество формул, однако, в данном методическом указании приводим лишь по одной, наиболее применимой. Для зоны гидравлически гладких труб можно воспользоваться формулой Блазиуса
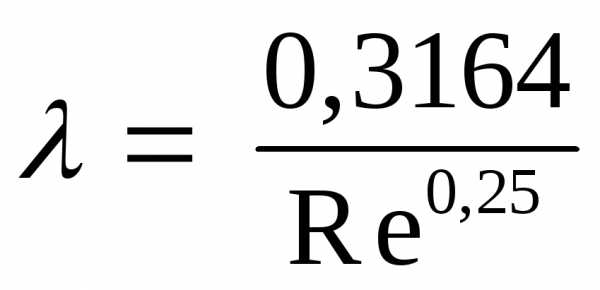 ;
(5)
;
(5)
4. З о н а д о к в а д р а т и ч н о г о с о п р о —
т и в л е н и я . Движение турбулентное. Ориентировочные границы зоны
,
где э- величина эквивалентной равномерно-зернистой шероховатости.
Под эквивалентной
шероховатостью понимают такую равномерно
— зернистую шероховатость, которая в
области квадратичного сопротивления
оказывает такое же сопротивление
движению жидкости как и труба с
естественной шероховатостью. В этой
зоне сопротивления коэффициент
гидравлического трения зависит от обеих
факторов  .
.
Для определения коэффициента гидравлического трения можно воспользоваться формулой А.Д. Альтшуля
. (6)
5. З о н а к в а д р а т и ч н о г о с о п р о т и в л е н и я.
Движение
турбулентное. Нижняя граница зоны 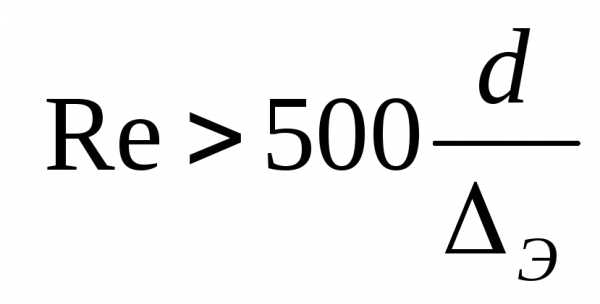 .
В этой зоне основным фактором, влияющим
на сопротивление, является шероховатость
стенок трубы
.
В этой зоне основным фактором, влияющим
на сопротивление, является шероховатость
стенок трубы 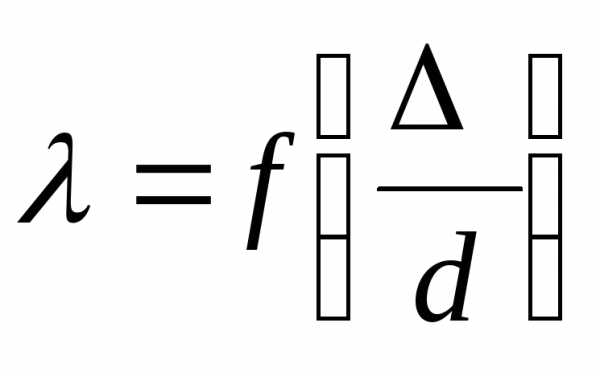 .
.
Для определения коэффициента гидравлического трения можно воспользоваться следующими формулой Б.Л.Шифринсона
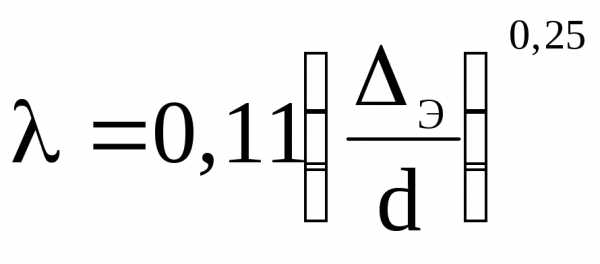 .
(7)
.
(7)
МЕТОДИКА ЭКСПЕРИМЕНТА
О п и с а н и е л а б о р а т о р н о й у с т а н о в к и
Схема лабораторной установки приведена на рисунке. Лабораторная установка состоит из напорного бака 1, исследуемой трубы 2 диаметром d. В начале и конце участка трубы длиной l через штуцеры и гибкие шланги 3 подключены пьезометры 4, снабженные измерительной шкалой. Расход воды в исследуемой трубе задается при помощи вентиля 5. Подача воды в напорный бак осуществляется по трубе 6 при помощи вентиля 7. Для измерения расхода воды служит мерный бак 8. Слив воды из мерного бака осуществляется по трубе 9 , открытием вентиля 10 . Температура воды измеряется термометром 11.
М е т о д и к а п р о в е д е н и я о п ы т о в
Перед проведением опытов напорный бак 1 заполняется водой. При этом вентиль 5 должен быть закрытым. Затем вентиль 5 открывается и задается расход Q в интервале 0 < Q <= Qmax. Обычно начинают с максимального расхода, соответствующего полному открытию вентиля 5. При проведении опытов необходимо поддерживать установившееся движение воды. Для этого при помощи вентиля 7 уровень воды в напорном баке 1
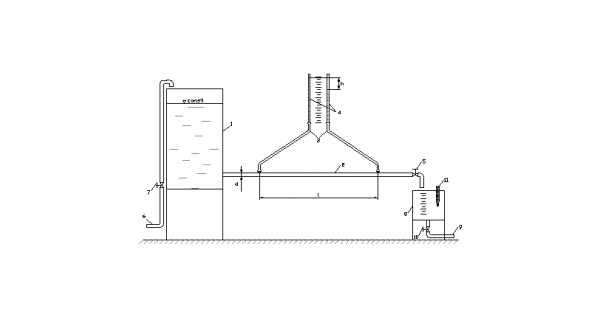
поддерживается постоянным. При заданном расходе воды выполняются следующие измерения. При помощи пьезометров 4 по шкале определяется разность уровней воды в них с погрешностью 0.5 мм. Линия визирования при этом должна быть перпендикулярна плоскости шкалы. Одновременно с этим определяется расход воды объемным способом при помощи мерной емкости 8 и секундомера
Температура жидкости необходима для определения кинематического коэффициента вязкости и измеряется в нижнем баке при помощи термометра с погрешностью ± 0,5 °С.
Расходы воды задаются с таким расчетом, чтобы в опытах охватить все зоны сопротивления.
ТРЕБОВАНИЯ БЕЗОПАСНОСТИ ТРУДА
1. Перед проведением опытов необходимо изучить инструкцию по правилам безопасности работы в лаборатории.
2. Изучить описание установки, подготовить необходимые приборы, выяснить непонятные вопросы у преподавателя. Приступать к проведению опытов только с разрешения преподавателя.
3. При проведении опыта аккуратно обращаться со стеклянными и хрупкими приборами и оборудованием лабораторной установки.
4. При возникновении затруднений в выполнении опытов, а также поломки приборов и оборудования, необходимо прекратить опыты и обратиться к преподавателю.
5. После завершения опытов доложить преподавателю и сдать приборы.
6. В случае получения травмы необходимо немедленно прекратить опыты и обратиться к преподавателю за медицинской помощью.
ПОРЯДОК ПРОВЕДЕНИЯ ОПЫТОВ
1. Подготовка установки к проведению опыта.
1.1. Открыть вентиль 7 и заполнить напорный бак 1 водой до уровня перелива напорного бака. При этом вентиль 5 должен быть закрытым.
1.3. Проверяется отсутствие течей воды в местах соединения гибких шлангов 3 и через вентили.
1.4. Определяются длина исследуемой трубы, внутренний диаметр, шероховатость стенок.
1.5. Определяют размеры мерной емкости.
2. Определение коэффициентов гидравлического трения опытным путем.
Максимальным открытием вентиля 5 устанавливают максимальный расход воды в трубе.
При помощи вентиля 7 добиваются постоянства уровня воды в напорном баке 1.
2.3. После достижения установившегося режима движения по шкале определяют разность уровней воды в пьезометрах 4. Результат записывают в таблицу.
2.4. Одновременно определяют расход воды объемным способом и измеряют температуру воды. При измерении расхода определяют время наполнения заданного объема мерной емкости.
2.6. После завершения всех измерений в данном опыте закрывается сначала вентиль 7, затем вентиль 5.
2.7. В таблице выполняются необходимые расчеты для установления зоны сопротивления .
2.8. Открывают вентиль 5 менее максимального, затем при помощи вентиля 7 добиваются постоянства уровня воды в напорном баке. Выполняют измерения аналогично первому опыту.
2.9. При проведении опытов добиваются, чтобы охватить все зоны сопротивления. Количество опытов должно быть не менее четырех.
2.10. После завершения всех опытов вентили 7 и 5 закрываются, вентиль 10 открывается и проверяется на отсутствие течей в вентилях, в местах соединения шлангов и в самих шлангах.
ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА
Результаты измерений и необходимых вычислений заносятся в таблицу.
1. Вычисляется площадь поперечного сечения трубы S:
 (8)
(8)
где d — внутренний диаметр трубы, см.
2. Вычисляется расход жидкости Q , см3/с.
 ,
(9)
,
(9)
где W — объем мерного сосуда, см3 ;
t — время наполнения мерного бака, с.
3. Вычисляется средняя скорость потока жидкости V:
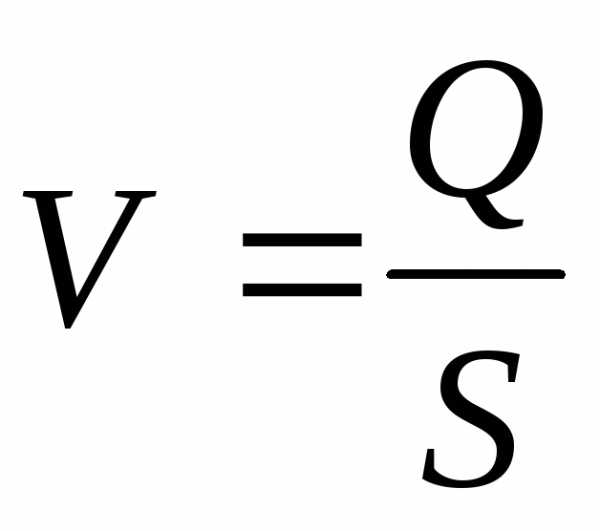 ,
,  .
(10)
.
(10)
4. Из приложения определяют кинематический коэффициент вязкости воды n см2 /с в соответствии с измеренной температурой °С.
5. Вычисляют число Рейнольдса Re, соответствующее каждому опыту и устанавливают зону гидравлического сопротивления:
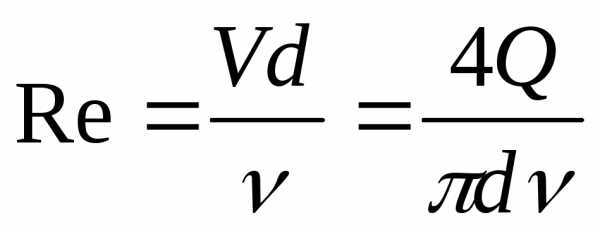 (11)
(11)
6. Вычисляют опытное значение коэффициента гидравлического трения по формуле
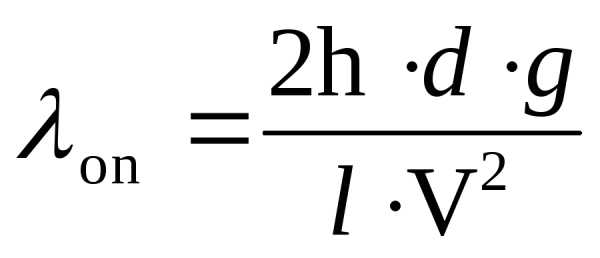 .
(12)
.
(12)
7 Вычисляют теоретическое значение коэффициента гидравлического трения по формуле, соответствующей зоне сопротивления .
8. Определяют расхождение коэффициентов гидравлического трения
 .
.
9. Делают выводы о соответствии теоретического и опытного коэффициентах гидравлического трения и характере изменения коэффициента в зависимости от числа Рейнольдса.
Определение погрешности эксперимента
Случайными погрешностями пренебрегают и рассматривают только систематические погрешности. Погрешность определения площади, расхода, скорости и коэффициента гидравлического трения находится как погрешность косвенных измерений.
Согласно выражениям (8) — (12), относительная погрешность определения площади, расхода, скорости и коэффициента гидравлического трения составит:
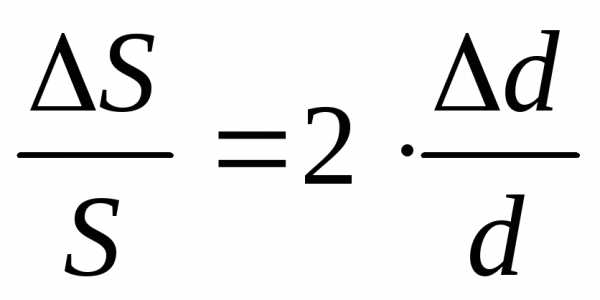 ,
(13)
,
(13)
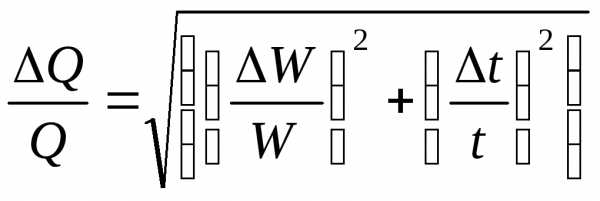 ,
(14)
,
(14)
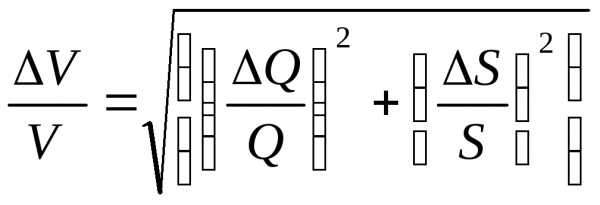 ,
(15)
,
(15)
, (16)
Через  обозначены абсолютные ошибки измерения
отдельных величин, входящих в выражения.
обозначены абсолютные ошибки измерения
отдельных величин, входящих в выражения.
В данной работе экспериментально измеряется время наполнения мерной емкости, уровень воды в пьезометрах и её температура.
Объем мерного сосуда определяют с погрешностью DW = ± 10 см3, время его наполнения с погрешностью Dt = ± 0,2 с, Погрешность кинематического коэффициента вязкости воды n определить в соответствии с погрешностью измерения температуры. Температуру воды определяют при помощи термометра с погрешностью ± 0,5 °С. Внутренний диаметр трубы измеряется по дубликату при помощи штангенциркуля с погрешностью не более 0,1 мм.
Погрешности по формулам (13 — 16) рассчитываются для каждого сопротивления и всех опытов. Далее делается анализ полученных результатов, намечаются пути увеличения точности опытов. По согласованию с преподавателем каждым студентом звена делается расчет одного из предложенных мероприятий по снижению погрешности. По результатам всех расчетов делается общий вывод о возможности увеличении точности опытов до заданной преподавателем величины.
СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА ПО РАБОТЕ
Отчет по работе каждым студентом оформляется письменно в отдельной тетради и должен содержать :
1. Название лабораторной работы.
2. Формулировку цели работы.
3. Некоторые основные понятия и формулы.
4. Схему и описание лабораторной установки.
5. Таблицу с результатами опыта.
6. Выводы.
При рукописном оформлении схема установки, таблицы выполняются в карандаше с использованием чертежных приборов. Желательно выполнение отчета полностью на компьютере.
studfile.net
Определение коэффициента гидравлического трения прямой трубы
Министерство образования и науки Российской Федерации
Национальный исследовательский ядерный университет «МИФИ»
Балаковский инженерно-технологический
Методические указания к выполнению лабораторной работы
по дисциплинам: «Гидравлика», «Механика жидкости и газа», «Водоснабжение и водоотведение с основами гидравлики», «Гидрогазодинамика», «Гидравлика и гидропневмопривод»
для студентов направлений: «Теплоэнергетика и теплотехника», «Строительство», «Конструкторско-технологическое обеспечение машиностроительных производств», «Строительство уникальных зданий и сооружений» », «Наземные транспортно-технологические средства»
профиль «Подъемно-транспортные, строительные, дорожные средства и оборудование»
очной, заочной и заочно-сокращенной форм обучения
Балаково 2015
Ц е л ь р а б о т ы:
1.Определить опытным путем коэффициент гидравлического трения.
2.Определить коэффициент гидравлического трения по теоретическим формулам и сравнить с опытным значением.
ОСНОВНЫЕ ПОНЯТИЯ
Потеря напора на трение по длине круглых труб hl oпределятся по формуле Дарси:
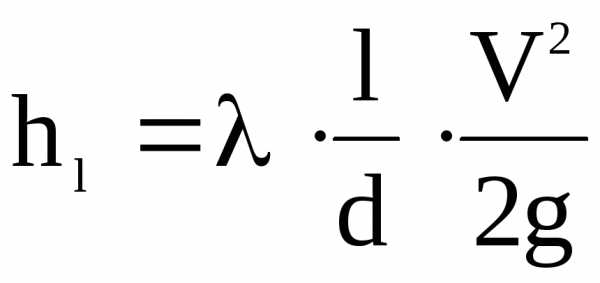 ,
(1)
,
(1)
где — коэффициент гидравлического трения;
l — длина трубы, на которой определяется потеря напора на трение;
d — диаметр трубы ;
V — средняя скорости жидкости;
g — ускорение силы тяжести, равное 981 см/с2 .
Многочисленными
экспериментами установлено, что
коэффициент гидравлического трения
зависит в общем случае от числа Рейнольдса
Re и относительной шероховатости стенок
трубы  :
:
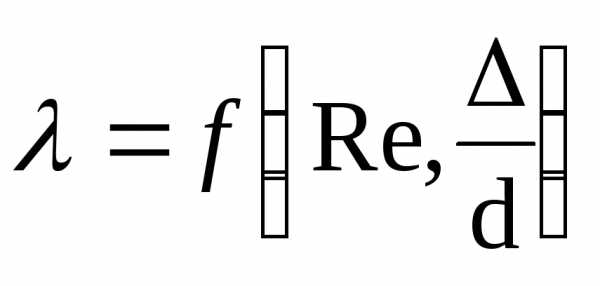 ,
(2)
,
(2)
где — высота выступов шероховатости внутренних стенок трубы.
Преобладание того или иного фактора зависит от режима течения жидкости.
Существует пять зон гидравлического сопротивления.
1. З о н а в я з к о г о с о п р о т и в л е н и я.
Движение ламинарное, Re < 2300. В этой зоне шероховатость стенок мало влияет на потери напора
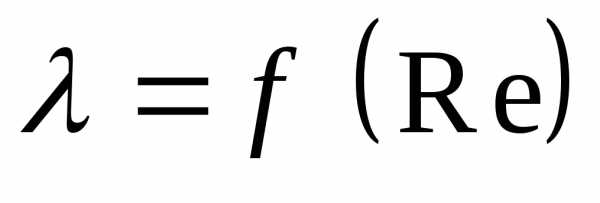 .
(3)
.
(3)
Теоретическая формула для определения коэффициента гидравлического трения для круглой трубы вытекает из закона Пуазейля :
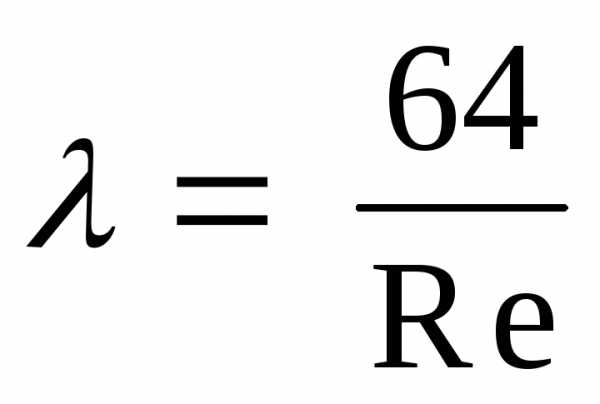 .
(4)
.
(4)
2. П е р е х о д н а я з о н а. При 2300 < Re < 4000 имеет место переходная зона, в которой движение уже не ламинарное и еще не турбулентное, т. е. здесь режим неустойчивый. Инженерные расчеты в этой зоне выполняются очень редко.
3. З о н а г
и д р а в л и ч е с к и г л а д к
и х т р у б. Движение турбулентное
4000 < Re < 105 . В этой зоне шероховатость стенок трубы
мало влияет на потери напора  .
.
Для определения коэффициента гидравлического трения существует множество формул, однако, в данном методическом указании приводим лишь по одной, наиболее применимой. Для зоны гидравлически гладких труб можно воспользоваться формулой Блазиуса
 ;
(5)
;
(5)
4. З о н а д о к в а д р а т и ч н о г о с о п р о —
т и в л е н и я . Движение турбулентное. Ориентировочные границы зоны
,
где э- величина эквивалентной равномерно-зернистой шероховатости.
Под эквивалентной шероховатостью понимают такую равномерно — зернистую шероховатость, которая в области квадратичного сопротивления оказывает такое же сопротивление движению жидкости как и труба с ес
diplomconsult.ru
11. Потери напора по длине. Порядок определения коэффициента трения.
Потери напора по длине иначе называют потерями напора на трение, возникают в гладких прямых трубах с постоянным сечением при равномерном течении. Такие потери обусловленны внутренним трением в жидкости и поэтому происходит и в шероховатых трубах, и в гладких. Основной расчетной формулой для потерь напора при ламинарном и турбулентном режиме движения в круглых трубах является формула Вейсбаха-Дарси
V-средняя скорость движения
Коэффициент трения зависит от числа Рейнольдса и от безразмерного геометрического фактора- относительной шероховатости (- абсолютное значение эквивалентной шероховатости )
Коэффициент трения при ламинарном режиме движения жидкости
Область турбулентного и переходного режимов разбиваются на 3 области :
1) область гидравлически гладких труб
2) область доквадратического сопротивления шероховатых труб
3) область квадратичного сопротивления шероховатых труб f
При турбулентном режиме движения жидкости коэффициент движения определяется по графику Мурина и по формуле Альтшуля
относительная шероховатость трубопровода
относительная гладкость трубопровода
Величину абсолютной эквивалентной шероховатости при расчетах берут из справочника в зависимости от материала труб и состояния его внутренней поверхности.
12.Местные гидравлические сопротивления. Потери напора на местных сопротивлениях.
Местные сопротивления это такие участки трубопровода, на которых происходит деформация потока, т.е. происходит изменения скорости потока или по величине или по направлению.
К местным сопротивлениям относятся: вход и выход потока из трубы, внезапные сужения и расширения труб, плавные сужения и расширения труб колена, отводы, тройники, диафрагмы, регулирующие устройства (краны, вентили, задвижки и т.д)
Протекая через местное сопротивление, поток деформируется, возникают пульсации скоростей и давлений, образуются вихревые зоны с обратными токами вследствие отрыва потока от стенок трубопровода. На эти процессы смешения и вихреобразования тратится часть полной энергии потока, которая превращается в тепло и рассеивается в окружающее пространство.
Различают четыре вида местных сопротивлений
Местные сопротивления на которых происходит изменение скорости по величине (рис.25 на стр.52)
Местные сопротивления связанные с изменением направления движения жидкости (рис. 26 на стр.52)
Местные сопротивления на которых происходит смешение или разделение потока(рис.27 на стр. 53)
Трубопроводная арматура(краны, вентили, задвижки, расходомеры и т.п.)
Потери напора на местном сопротивлении рассчитываются в долях от величины скоростного напора:
где-коэффициент местного сопротивления,
v-скорость движения жидкости, м/с
g-ускорение свободного падения, м/с^2
13.Виды потерь напора(давлений) в трубопроводах. Расчетные формулы.
Потери напора по длине потока. Иначе их называют потерями напора на трение, возникают в гладких прямых трубах с постоянным сечение при равномерном течении. Такие потери обусловлены внутренним трением в жидкости и поэтому происходят в шероховатых трубах, и в гладких.
где -коэффициент гидравлического трения,
l-длина трубопровода, м;
d-диаметр трубопровода, м;
v-средняя скорость движения жидкости, м/с;
g-ускорение свободного падения, м/с^2;
коэффициент трения зависит от числа РейнольдсаRe(режима движения жидкости) и от безразмерного геометрического фактора-относительной шероховатости (или-абсолютное значение эквивалентной шероховатости)
коэффициент трения при ламинарном режиме движения жидкости рассчитывается по формуле:
На практике при турбулентном режиме движения коэффициент трения может быть определен по графику Г.А.Мурина или рассчитан по формуле А.Д.Альтшуля:
Где Re-критерий Рейнольдса;
-коэффициент трения;
-абсолютное значение эквивалентной шероховатости, м;
d- диаметр трубопровода, м;
Потери напорана местное сопротивления.
Потери напора на местном сопротивлении рассчитываются в долях от величины скоростного напора:
где-коэффициент местного сопротивления,
v-скорость движения жидкости, м/с
g-ускорение свободного падения, м/с^2
Принцип сложения потерь напора.
Как правило, трубопроводы имеют прямые участки и множество местных сопротивлений. Принцип сложения потерь напора заключается в том, что потери напора по длине и потери напора на местных сопротивлениях складываются, т.е общие потери напора:
т.е
где где -коэффициент гидравлического трения,
l-длина трубопровода, м;
d-диаметр трубопровода, м;
v-средняя скорость движения жидкости, м/с;
g-ускорение свободного падения, м/с^2;
-сумма коэффициентов местных сопротивлений.
Часто в расчетах требуется определить потерю давления .
Потеря давления в трубопроводе на трение(для участка прямого трубопровода, длинного трубопровода), вычисляется по формуле
studfile.net
Коэффициент гидравлического сопротивления трения труб
Гидравлические потери или гидравлическое сопротивление — безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (систем гидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения.
Калькулятор расчета коэффициента гидравлического сопротивления трения труб
| Расход жидкости | |
| Коэффициент кинематической вязкости ( для воды тем-рой 100C = 1,3, 200C = 1) | |
| Диаметр трубопровода | |
| Длина трубопровода | |
| Плотность жидкости | |
| Коэффициент шероховатости стенок трубопровода | |
| Выберите тип трубопроводаЦельнотянутые (Латунь-Медь-Сталь)Цельнотянутые (Стальные новые)Цельнотянутые стальные(Б\У)Цельносварные стальныеКлепаные стальныеИз кровельной сталиОценкованые стальныеЧугунные новыеЧугунные водопроводыеЖелезобетонные новыеАсбстоцементныеСтеклянныеЖелезобетонные | |
| Режим течения | |
| Скорость движения жидкости в трубопроводе, м/c | |
| Число Рейнольдса (Re) | |
| Коэффициент трения (λ) | |
| Коэффициент гидравлического сопротивления (ξ) | |
| Потеря давления (Δp), Па | |
0
0
Было ли это полезно?Гидравлические потери принято разделять на два вида:
- потери на трение по длине — возникают при равномерном течении, в чистом виде — в прямых трубах постоянного сечения, они пропорциональны длине трубы;
- местные гидравлические потери — обусловлены т. н. местными гидравлическими сопротивлениями — изменениями формы и размера канала, деформирующими поток. Примером местных потерь могут служить: внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п.
Во многих случаях приближённо можно считать, что потери энергии при протекании жидкости через элемент гидравлической системы пропорциональны квадрату скорости жидкости. По этой причине удобно бывает характеризовать сопротивление безразмерной величиной ζ, которая называется коэффициент потерь или коэффициент местного сопротивления и такова, что
То есть в предположении, что скорость w по всему сечению потока одинакова, ζ=Δp/eторм, где eторм = ρw²/2 —энергия торможения единицы объёма потока относительно канала. Реально в потоке скорость жидкости не равномерна, в справочной литературе в данных формулах принимается среднерасходная скорость w=Q/F, где Q — объёмный расход, F — площадь сечения, для которого рассчитывается скорость[1]. Таким образом, средняя энергия торможения потока обычно несколько больше ρw²/2, см. Среднее квадратическое.
Для линейных потерь обычно пользуются коэффициентом потерь на трение по длине (также коэффициент Дарси) λ, фигурирующего в формуле Дарси — Вейсбаха
где L — длина элемента, d — характерный размер сечения (для круглых труб это диаметр). Иначе в единицах давления
таким образом, для линейного элемента относительной длины L/d коэффициент сопротивления трения ζтр=λL/d.
Связанные Калькуляторы
wpcalc.com
Гидравлические сопротивления
4.5. Местные гидравлические сопротивления
Все гидравлические потери энергии делятся на два типа: потери на трение по длине трубопроводов (рассмотрены в п.4.3 и 4.4) и местные потери, вызванные такими элементами трубопроводов, в которых вследствие изменения размеров или конфигурации русла происходит изменение скорости потока, отрыв потока от стенок русла и возникновение вихреобразования.
Простейшие местные гидравлические сопротивления можно разделить на расширения, сужения и повороты русла, каждое из которых может быть внезапным или постепенным. Более сложные случаи местного сопротивления представляют собой соединения или комбинации перечисленных простейших сопротивлений.
Рассмотрим простейшие местные сопротивления при турбулентном режиме течения в трубе.
1. Внезапное расширение русла. Потеря напора (энергии) при внезапном расширении русла расходуется на вихреобразование, связанное с отрывом потока от стенок, т.е. на поддержание вращательного непрерывного движения жидких масс с постоянным их обновлением.
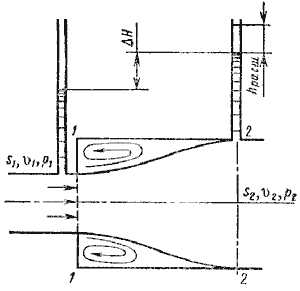
Рис. 4.9. Внезапное расширение трубы
При внезапном расширении русла (трубы) (рис.4.9) поток срывается с угла и расширяется не внезапно, как русло, а постепенно, причем в кольцевом пространстве между потоком и стенкой трубы образуются вихри, которые и являются причиной потерь энергии. Рассмотрим два сечения потока: 1-1 — в плоскости расширения трубы и 2-2 — в том месте, где поток, расширившись, заполнил все сечение широкой трубы. Так как поток между рассматриваемыми сечениями расширяется, то скорость его уменьшается, а давление возрастает. Поэтому второй пьезометр показывает высоту на ΔH большую, чем первый; но если бы потерь напора в данном месте не было, то второй пьезометр показал бы высоту большую еще на hрасш. Эта высота и есть местная потеря напора на расширение, которая определяется по формуле:
где S1, S2 — площадь поперечных сечений 1-1 и 2-2.
Это выражение является следствием теоремы Борда, которая гласит, что потеря напора при внезапном расширении русла равна скоростному напору, определенному по разности скоростей
Выражение ( 1 — S1/S2 )2 обозначается греческой буквой ζ (дзета) и называется коэффициентом потерь, таким образом2. Постепенное расширение русла. Постепенно расширяющаяся труба называется диффузором (рис.4.10). Течение скорости в диффузоре сопровождается ее уменьшением и увеличением давления, а следовательно, преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α.

Рис. 4.10. Постепенное расширение трубы
Кроме того, в диффузоре имеются и обычные потери на терние, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых:
где hтр и hрасш — потери напора на трение и расширение (вихреобразование). где n = S2/S1 = ( r2/r1 ) 2 — степень расширения диффузора. Потеря напора на расширение hрасш имеет ту же самую природу, что и при внезапном расширении руслагде k — коэффициент смягчения, при α= 5…20°, k = sinα.
Учитывая это полную потерю напора можно переписать в виде:
откуда коэффициент сопротивления диффузора можно выразить формулой

Рис. 4.11. Зависимость ζдиф от угла
Функция ζ = f(α)имеет минимум при некотором наивыгоднейшем оптимальном значении угла α, оптимальное значение которого определится следующим выражением:
При подстановке в эту формулу λТ =0,015…0,025 и n = 2…4 получим αопт = 6 (рис.4.11).
3. Внезапное сужение русла. В этом случае потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока (рис.4.12).
gidravl.narod.ru
